形式语言与自动机
Induction 数学归纳法
regular language 正则语言
definition 定义
在字母表集合Σ上的正则语言定义如下:
- 空集合Ø是正则语言
- 只包含一个空串的语言{ε}是正则语言
- 对所有a∈Σ,{a}是正则语言
- 若A, B是正则语言,则$A \cdot B$,$A \bigcup B$,$A^*$都是正则语言
- 除此之外都不是正则语言
regular expression 正则表达式
regular expressions are a compact syntax for regular language
正则表达式是正则语言的紧凑语法
multiple regular expressions can denote the same language
多个正则表达式可以表示同一种语言,例如0+0、01+0、0都可以表示empty Ø
word over A={a,b} that have at least one a
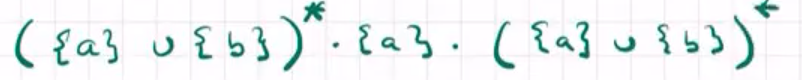
其中${ a}\bigcup { b}$不可以写成{a, b},因为单例集是基本的构建块(singleton sets are the basic building blocks)。但是可以化简成
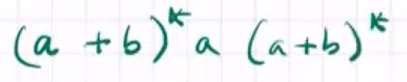
句法和语义的关系
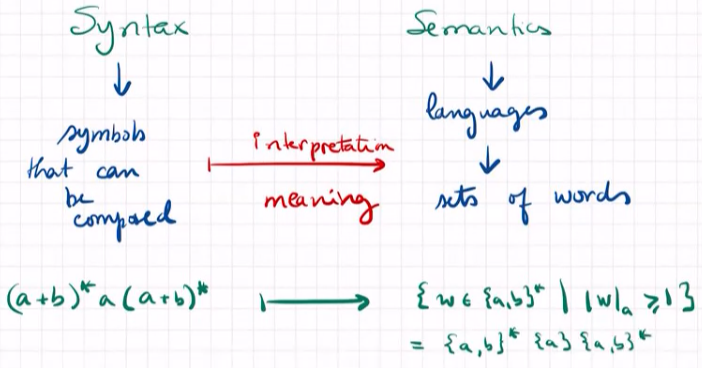
正则表达式与正则语言关系及相互转化

证明words starting with n a‘s and n b’s,$L={ a^nb^n|n∈N }$不是正则语言
Deterministic finite automata 确定有限状态自动机
Definition 定义
A DFA is a tuple$(Q,\delta,i,F)$

DFA接受word
a word $w∈A^*$ is accepted by a DFA$(Q,\delta,i,F)$ if $\delta ^*(i, w)=F$
DFA接受language

通过DFA归纳语言例子
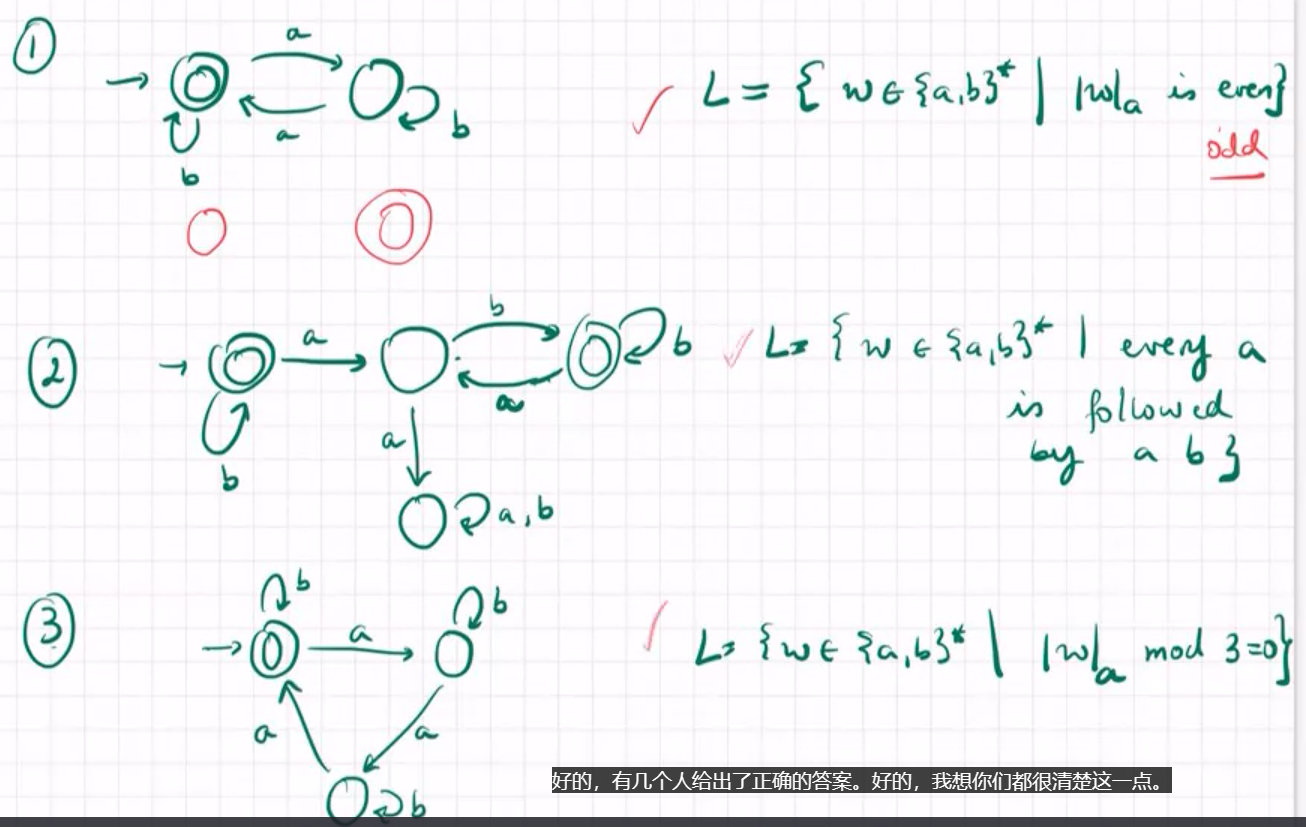
DFA are not the most efficient data structure DFA 不是最高效的数据结构

Q1: is the language regular?
yes
Q2: if regular what is the regular expression?
$(a+b)^*a(a+b)(a+b)(a+b)$
Q3: How many states would one need for DFA?
total 16 states
为什么DFA不能表示成下面的形式

- there are two a transitions
- state 1 has zero transition
nondeterministic finite automata 非确定有限状态自动机
缘由:DFA的状态转移总数会基于状态数呈现指数级增长
知识点:P(s) powerset of a set S S集合的幂集,是一个由S全部子集组成的集合,S={s1, s2},则P(S)={Ø, {s1}, {s2}, {s1, s2}}
definition 定义:

每个DFA也是一个NFA,根据定义{q}也是{q}的子集
there is always a equivalent DFA given an NFA 给定一个 NFA,总有一个等价的 DFA
word accepted by an NFA
there must be at least one path that accept the word

a word $w∈A^*$ is accepted by an NFA$(Q, i, \delta, F)$ if and only if

样例

Language accepted by an NFA NFA接受的语言

NFA with λ-transition
Goal: give NFAs the capability of selectiong a new state without reading a symbol.
$\delta:Q\times(A\cup\lambda)\rightarrow P(Q)$
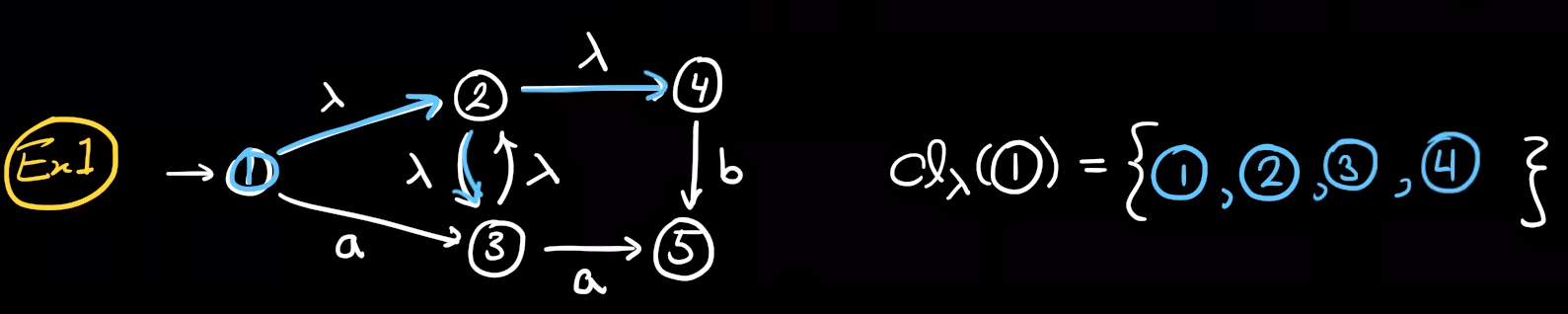
知识点:λ-closure λ闭包
given a state q∈Q in an NFA returns the set of states one can reach using only λ.
λ-closure(q) is the smallest subset of Q.


使用λ-NFA,我们现在可以轻松地为语言并集、顺序组合和星形$(+,\cdot,*)$构建自动机。
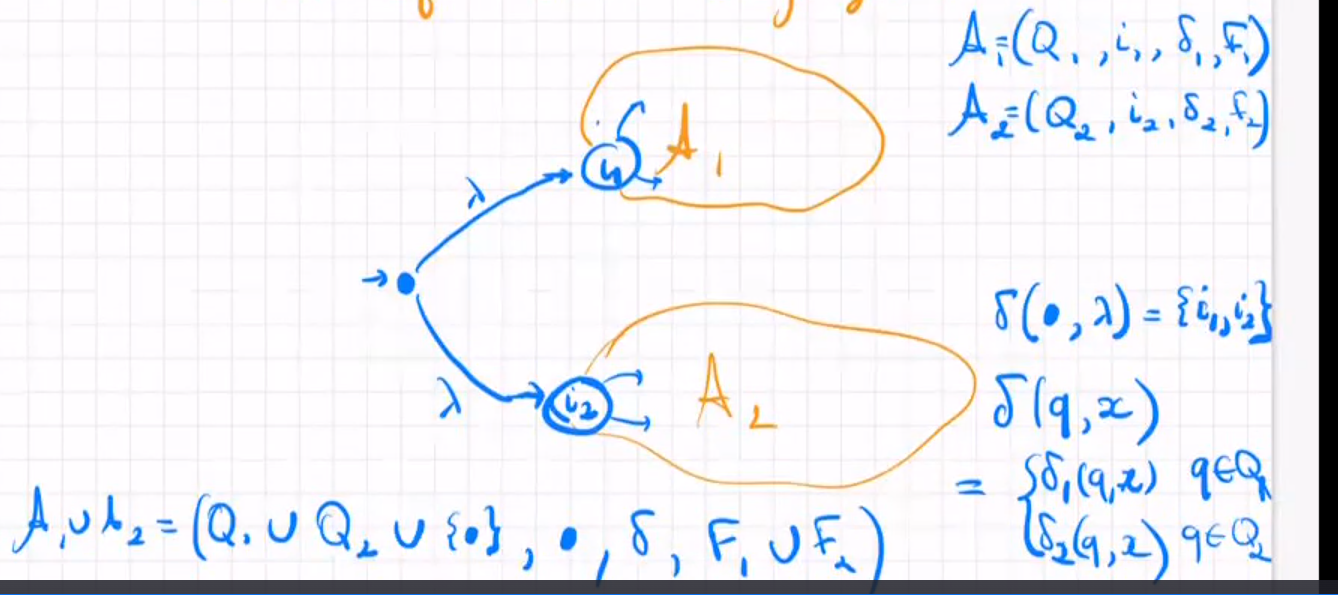

Regular expression -> NFA-λ -> NFA -> DFA转化
goal 1: how to eliminate lambda transitions
rule 1: given a state q in the automata, the state is final if q was already final or  可以仅使用λ到达最终状态
可以仅使用λ到达最终状态
rule 2: 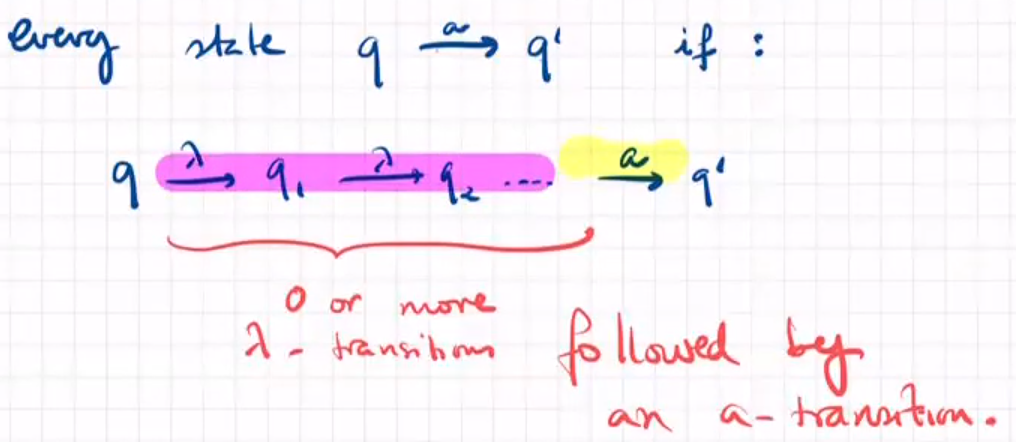
construction

可靠性定理证明

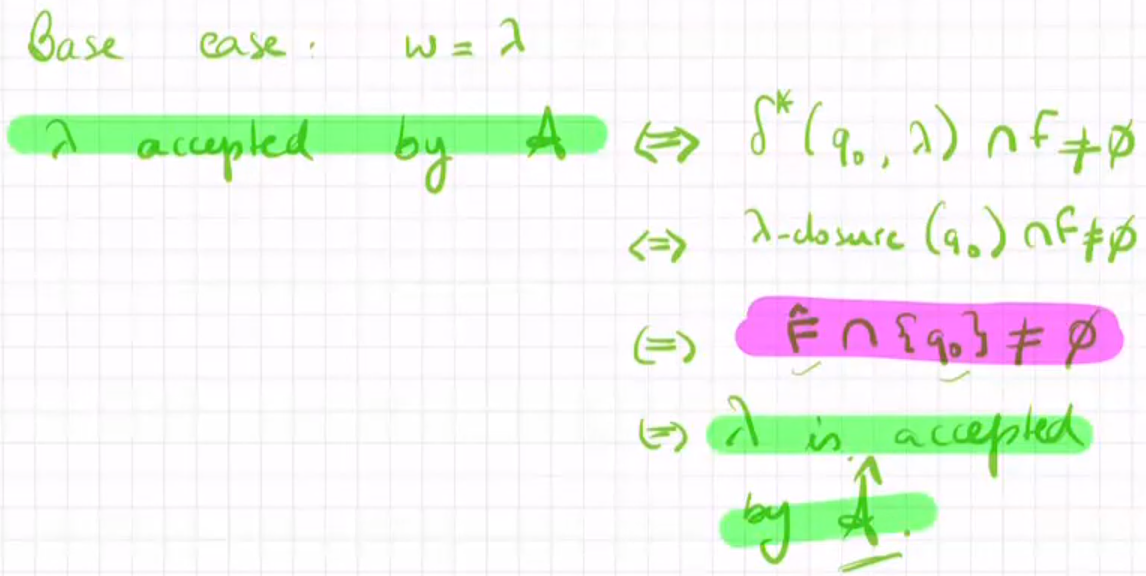


NFA-λ和NFA有着同样的表现力
goal 2: how to construct an equivalent DFA from a given NFA
construction

样例
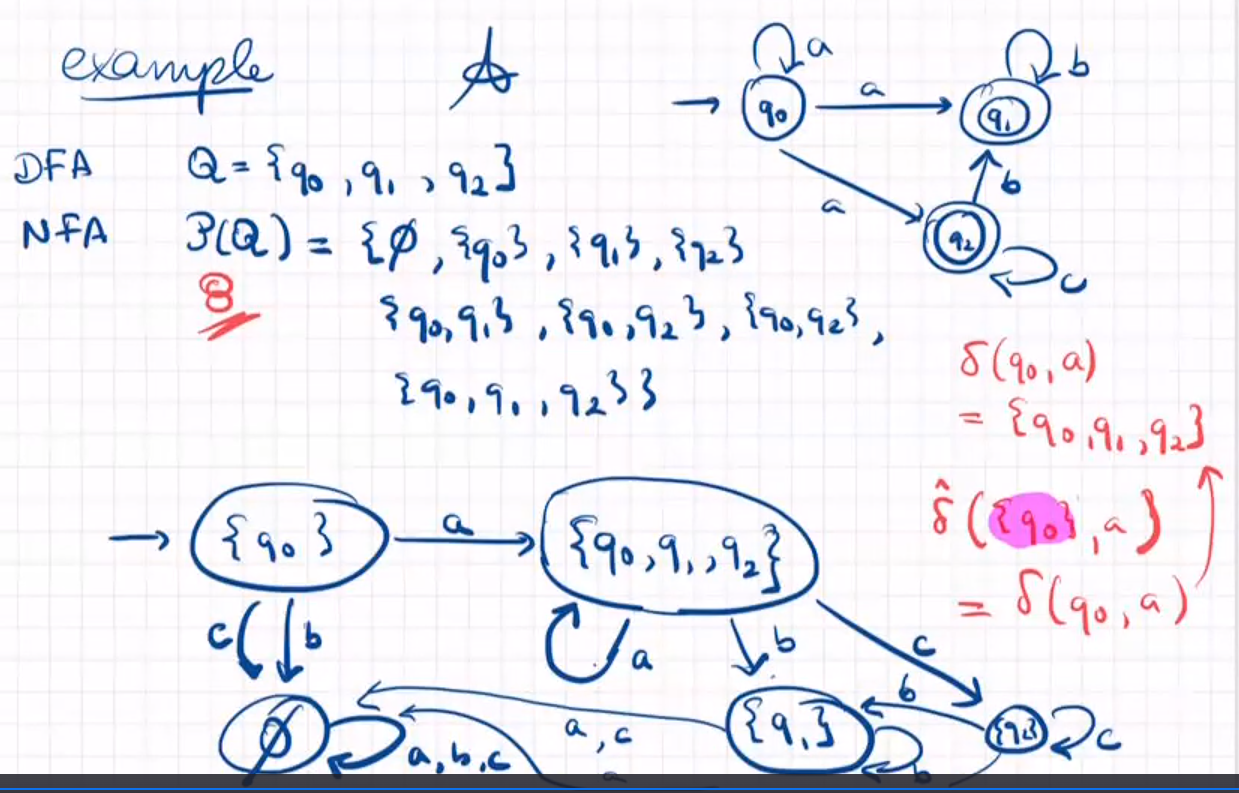
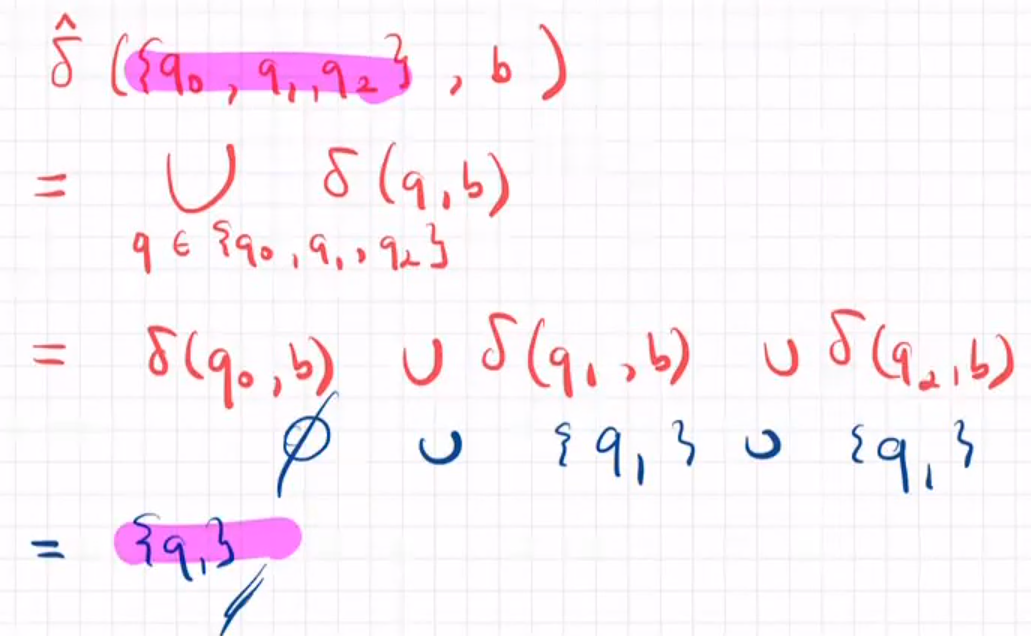
DFAs have $2^n$ states when building from NFAs but not all states are needed。因为不需要的状态无法从初始状态到达。对于一个有着n状态的NFA构建DFA,最坏情况是$|P(Q)|=2^n$
从NFA映射到DFA的结构有两个名称:subset construction 子集构造,determinisation 确定性
可靠性证明




chomsky hierarchy 语言体系
finite language 有限语言
regular language 正则语言
context-free language 上下文无关文法
context-concentive language 上下文相关文法
tree 数
DFA、NFA、NFA-lambda 有限状态自动机
pushdown automata 下推自动机
turing mechine 图灵机

kleene’s theorem
How to use kleene’s theorem to show that a language is not regular



proof of kleene’s theorem
DFA -> R.exp.:state-elimination algorithm 使用状态消解法
Take an automata with n states and delete state by state until having an automata with just two states.
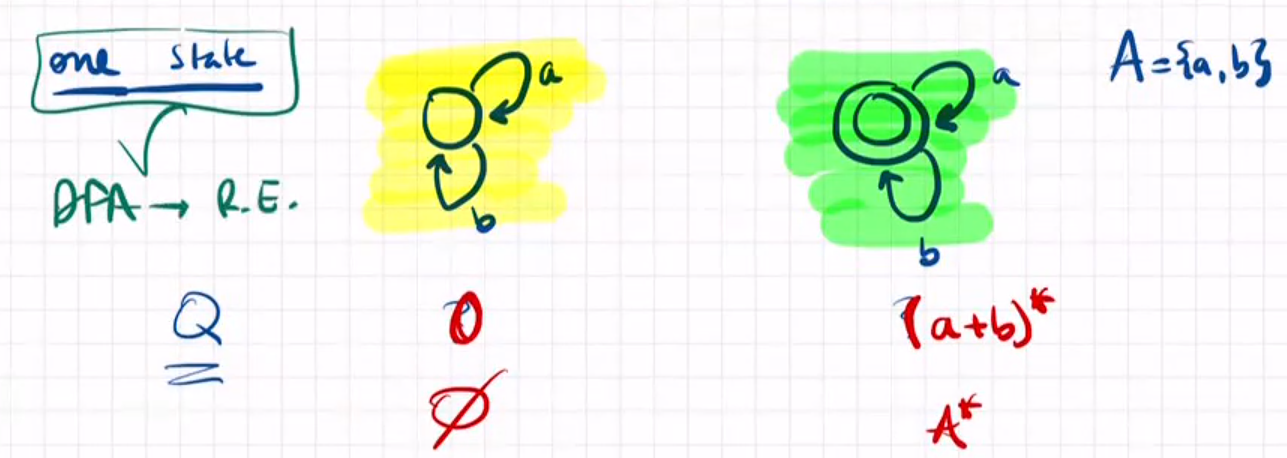
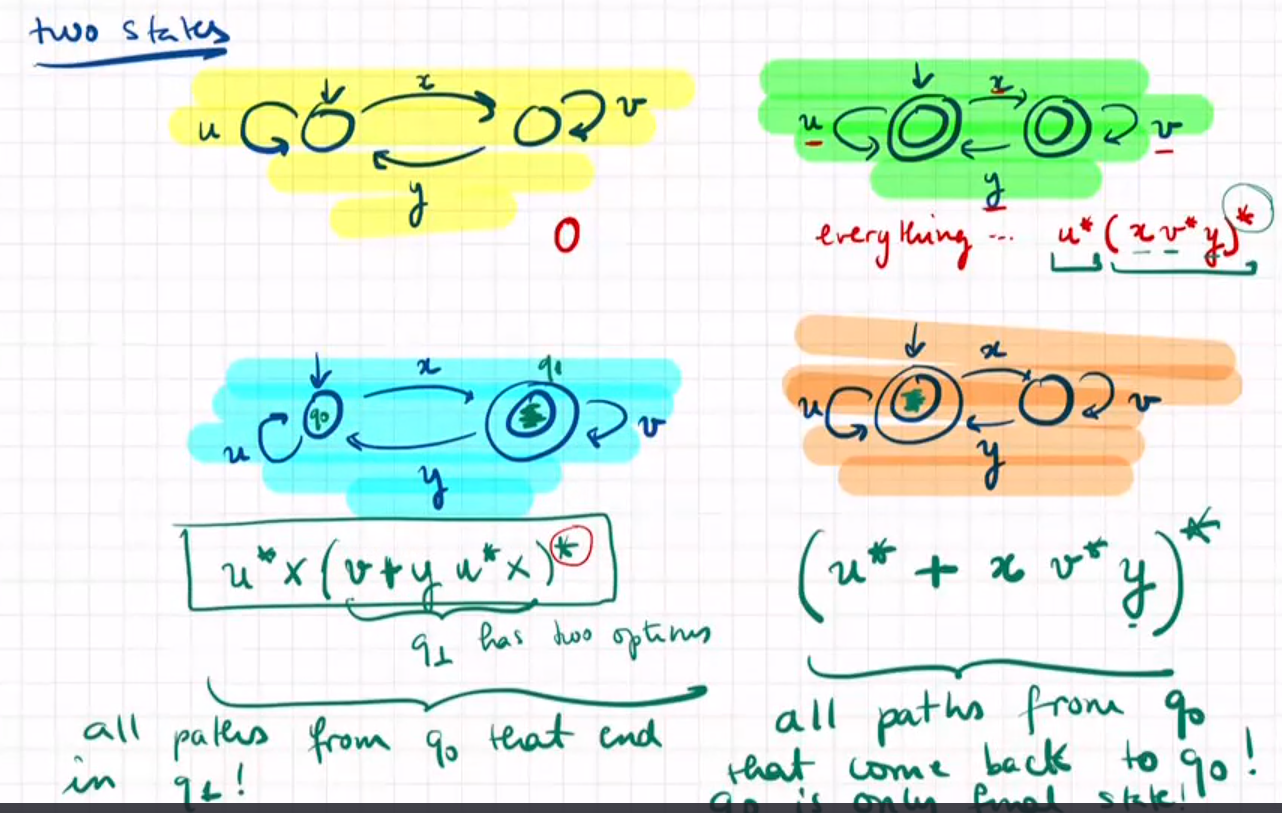

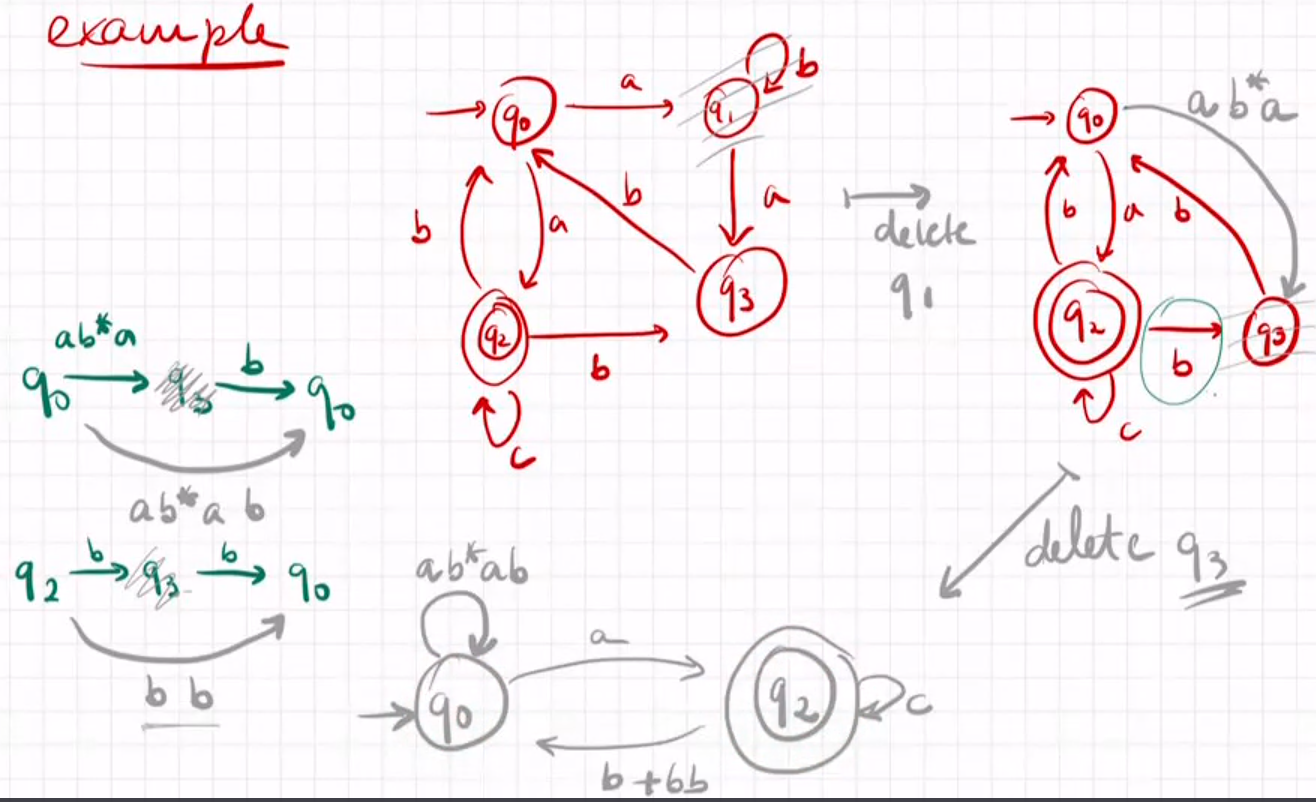
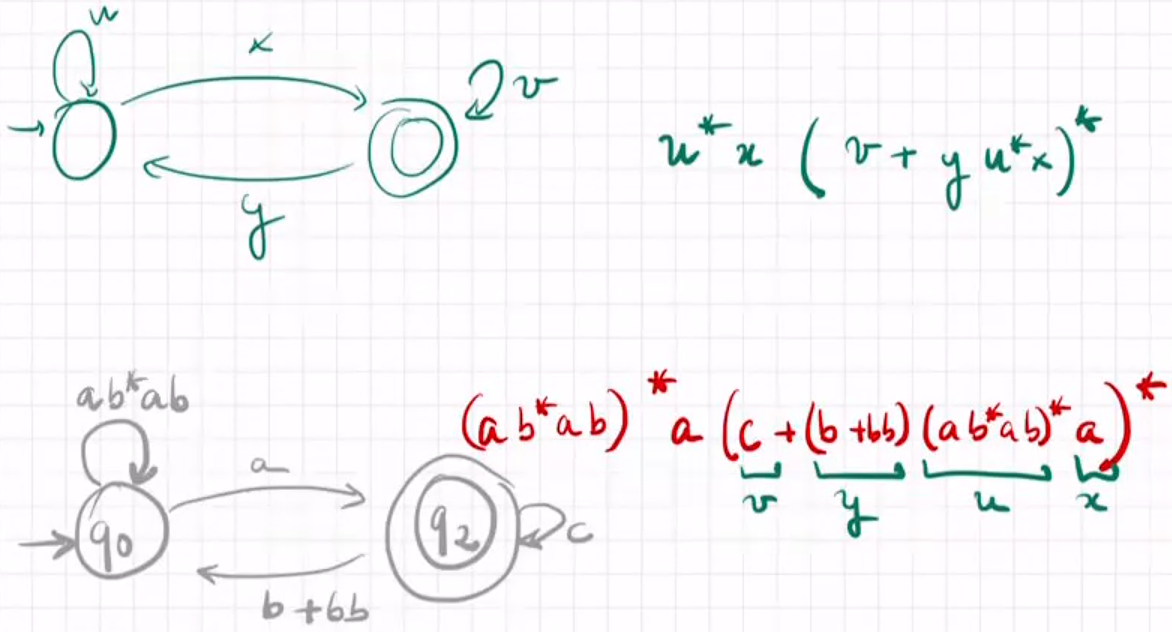
R.exp.->DFA:Brzozowski Derivative
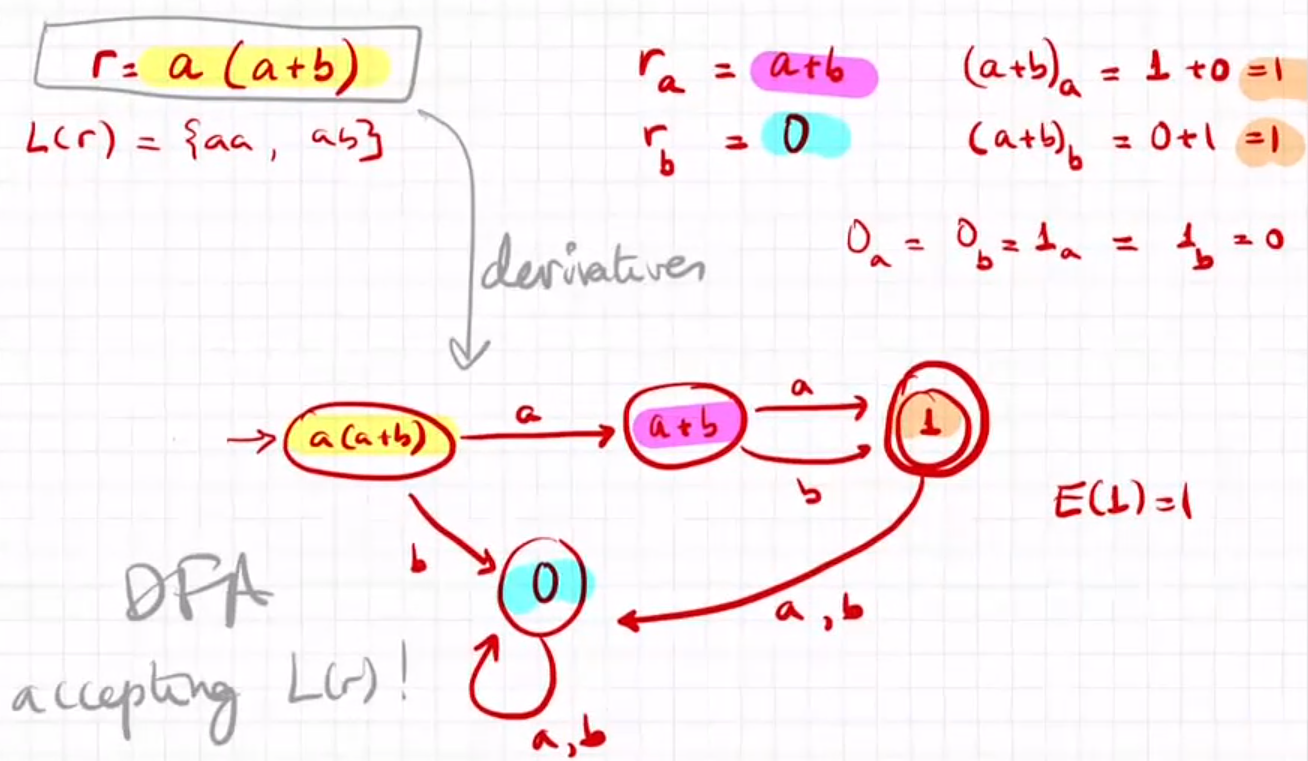
可以使用下面的方法,但是另一种方法Brzozowski Derivative可以直接转换
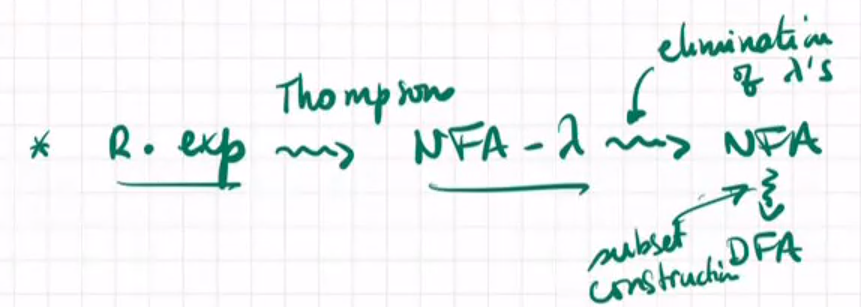
solution to a Linear system 针对线性系统的方法




Plan for today
closure properties of regular language 正则语言的闭包特性
$L^R$ is regular given L regular
根据kleene’s theorem,只需证明Produce a DFA for $L^R$ given a DFA for L
- swap initial an final states
- reverse all arrows

how to prove that a language is not regular: pumping lemma
if length of a word is long enough the path in the automata needs to visit same state over and over again

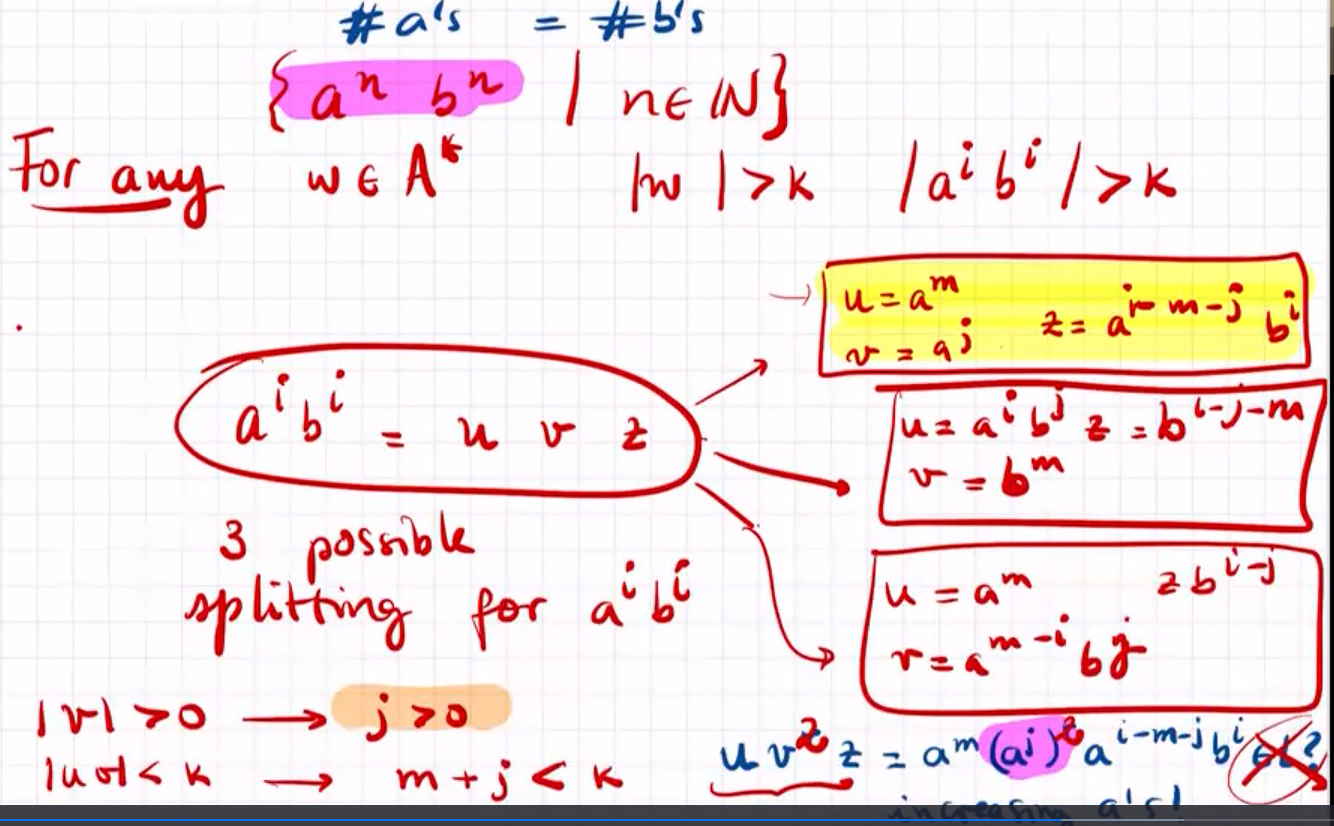
例题


context-free language 上下文无关语言
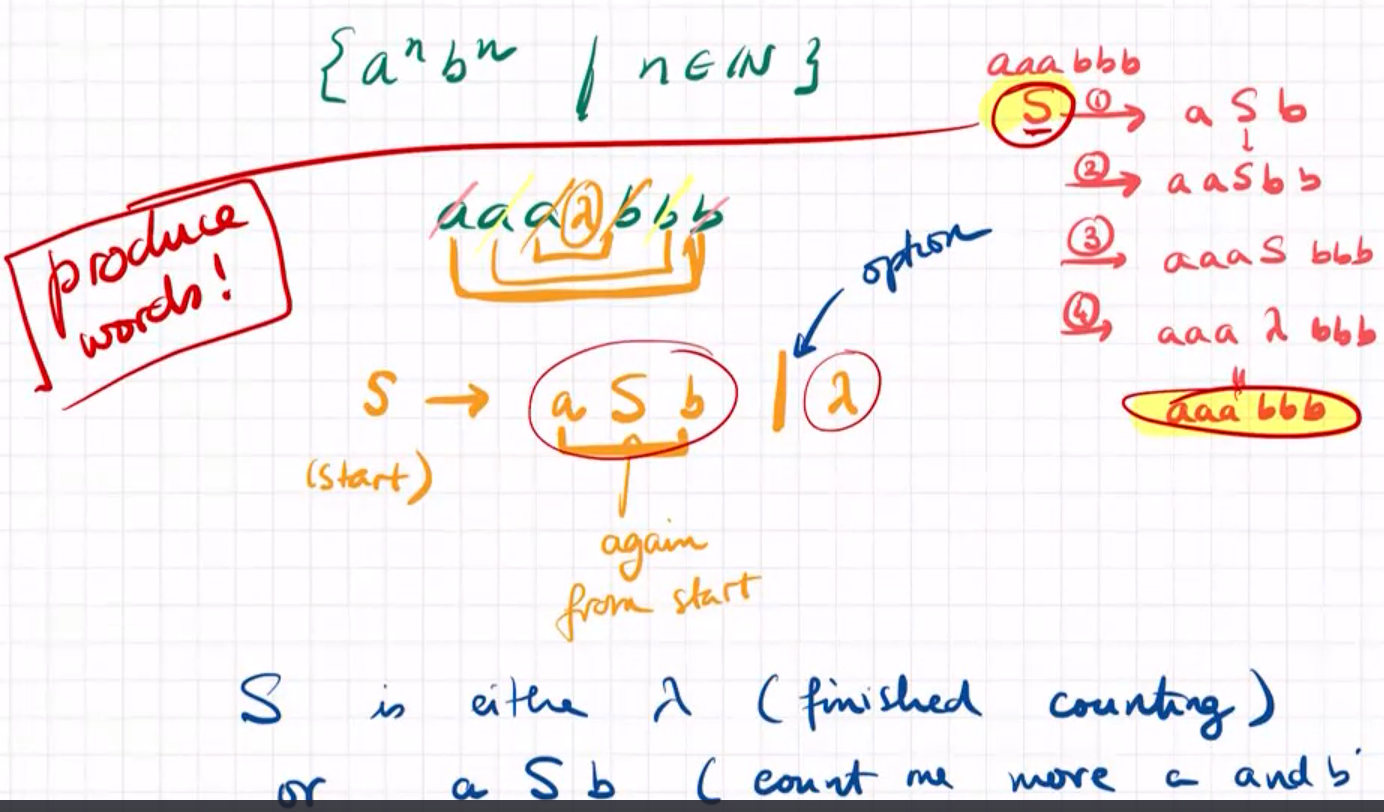
a CFG is a tuple(V, $\Sigma$, P, S)
V is a set of sumbols which we call terminal
$\Sigma$ is the alphabet(terminal symbols)
P a final set of rules. a rule is A->w where a∈ V, $w∈(V∪\Sigma)^*$
S∈V, starting symbol
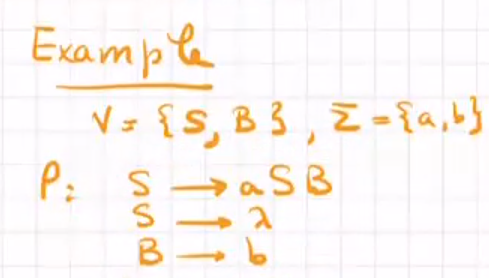
words generated by a grammer


language accepted/generate by grammar
given a grammar G=(V, $\Sigma$, P, S) the setof words or languages accepted by G:
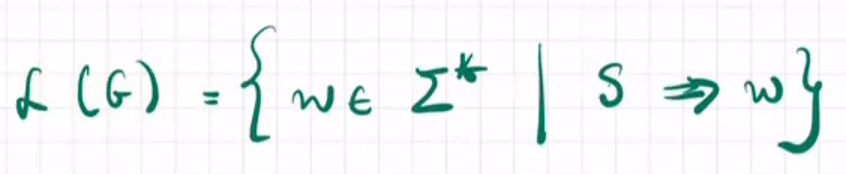
goal: prove $a^nb^n$ is generated by G for any n∈N

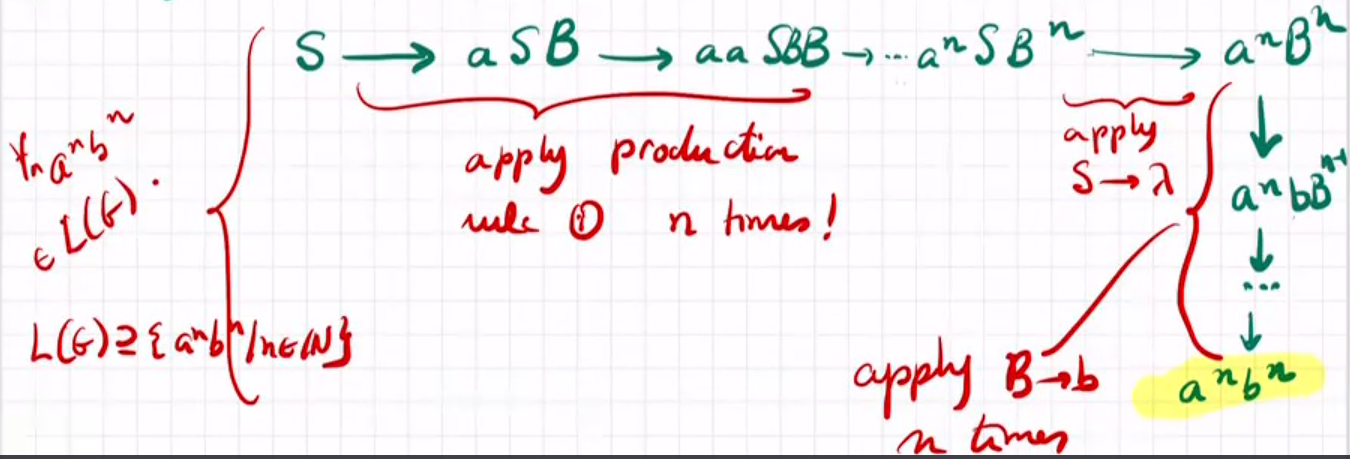



从语法生成words的不同策略(树结构)
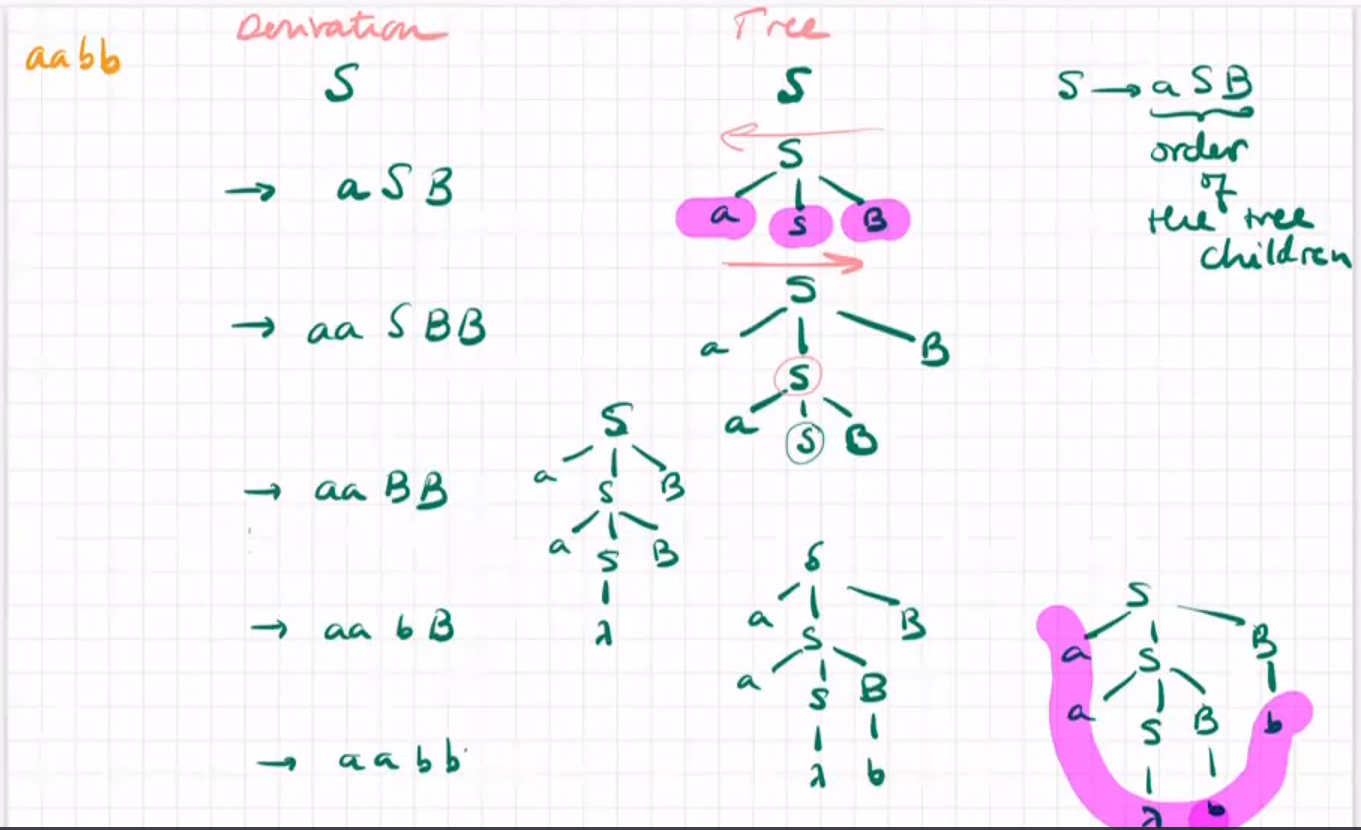
there are multiple left most derivations of the same word
S->aS->aa和S->Sa->aa都可以表示aa

pushdown automata for CFL
$L={a^nb^n|n∈N}$ is not regular, there is no finate ddeterministic automata accepting L, because we need to count a’s. We need automata with memory to count. Use stack.
defination



多个状态,多个堆栈

example
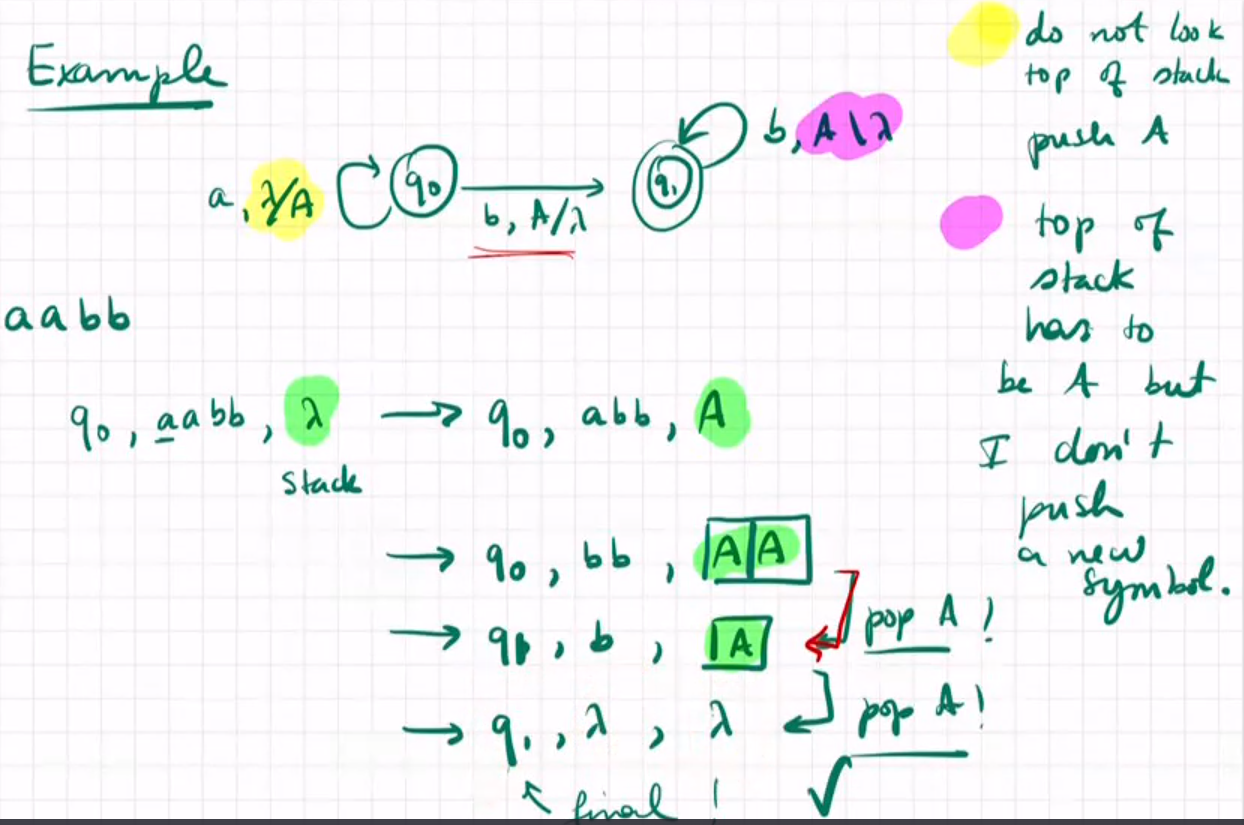

language accepted by a pushdown automata

state, word, stack = configuration of PDA
state where reading w start, start with an empty stack
acceptance by empty stack and final state
GOAL: Given a CFG build a pushdown automaton accepting the same language

转化图的定义不太正确
第一个与过渡的类型有关,允许多个符号推送到堆栈是一个错误。只允许检查堆栈的顶部,并写一个符号。这个问题可以通过分解状态解决
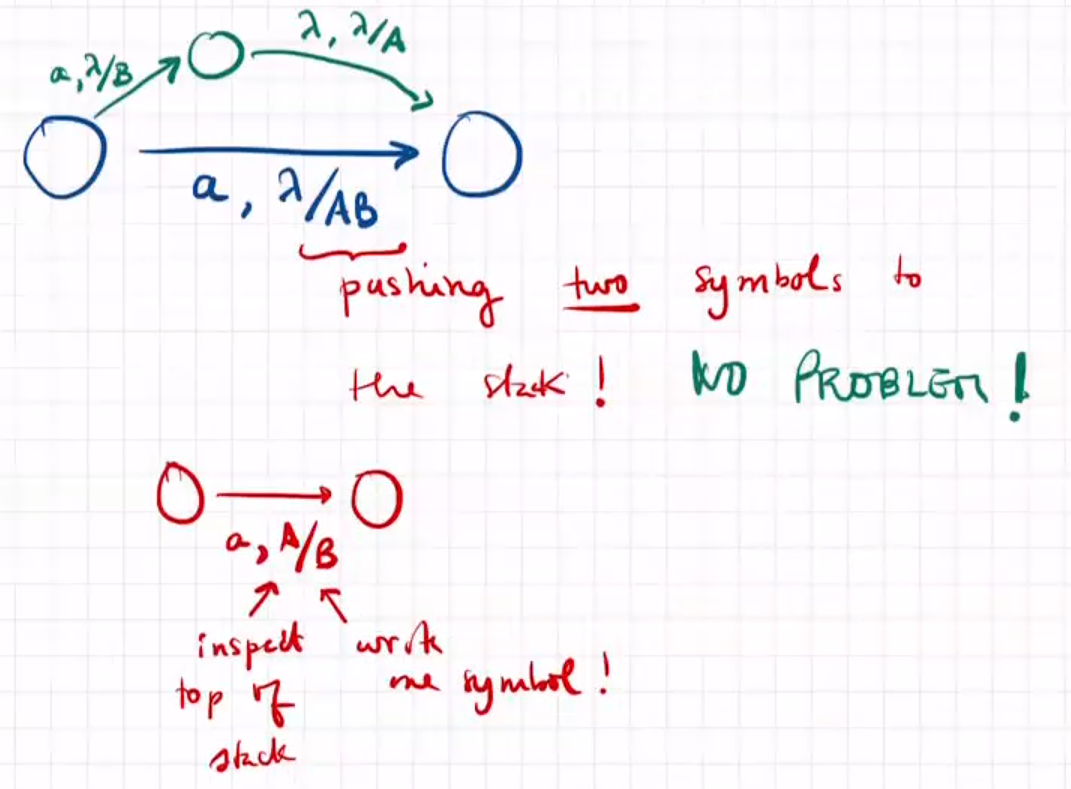
第二个问题是为所有非终端提供的所有生产规则都有终端。这些语法比较特殊





PDA->CFG


closure properties for CFL
facts CFL are closed under union, concaleation, and kleene star

facts CFL are not closed under intesection

pumping lemma for CFL
在上下文无关语法中拥有的每一棵树都将具有最大深度,因此,我们不是像对常规语言那样查看字符串的长度,而是查看生成树的深度。


习题课
DFA
问题一:Design a DFA that accepts the language
例一:
解答:
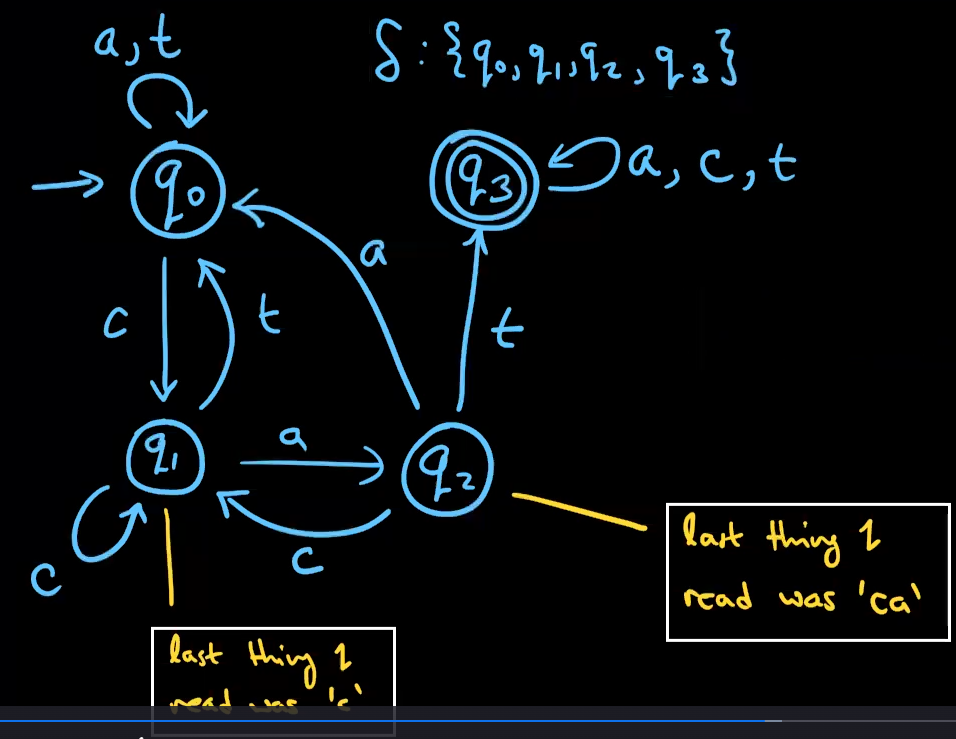
例二:

解答:

例三:

NFA

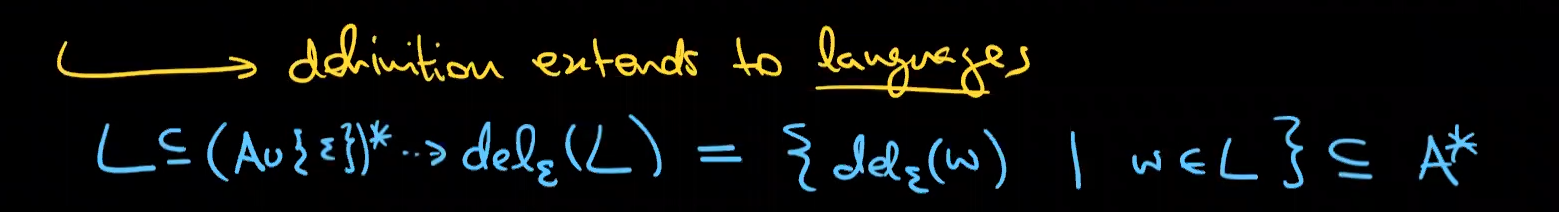
nfa-λ
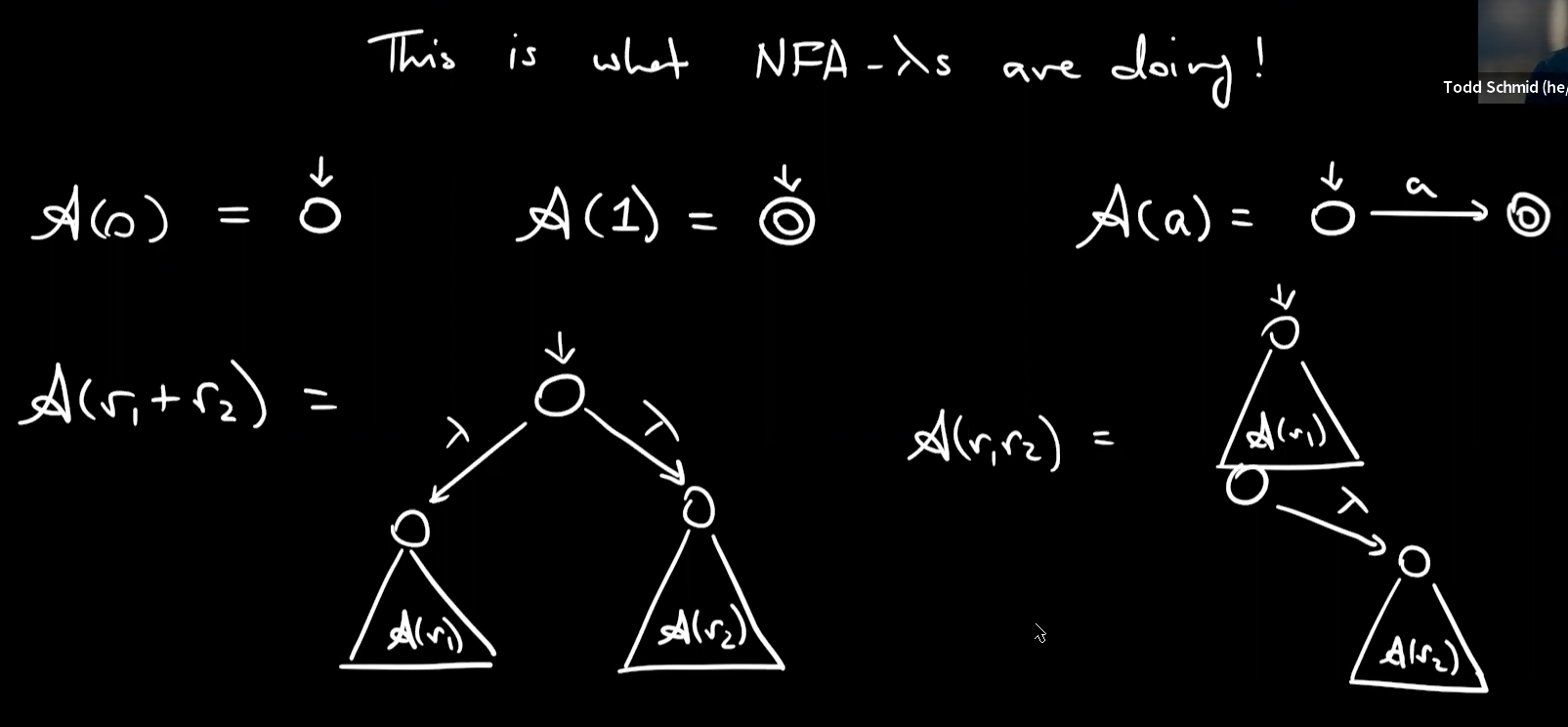
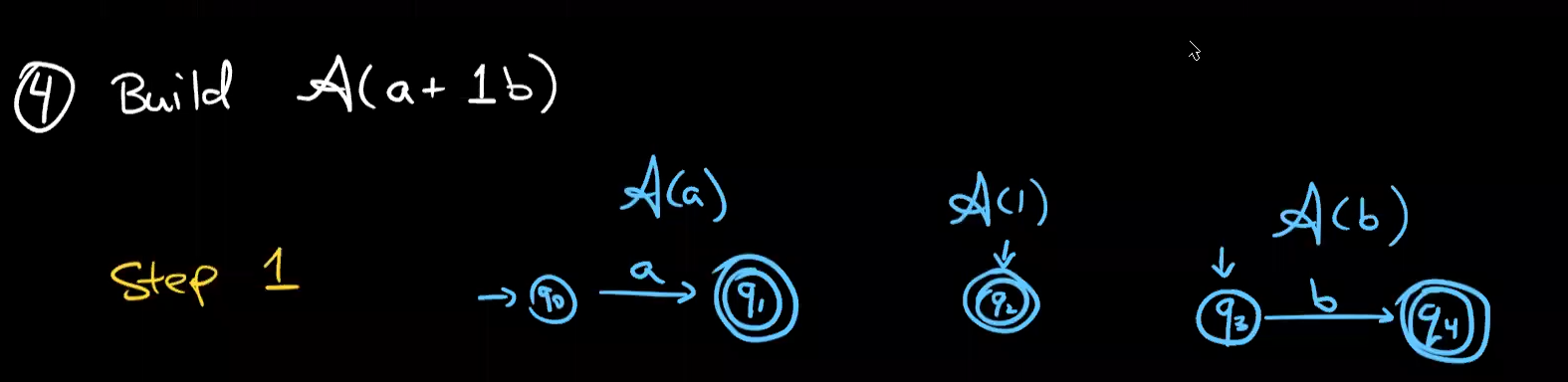
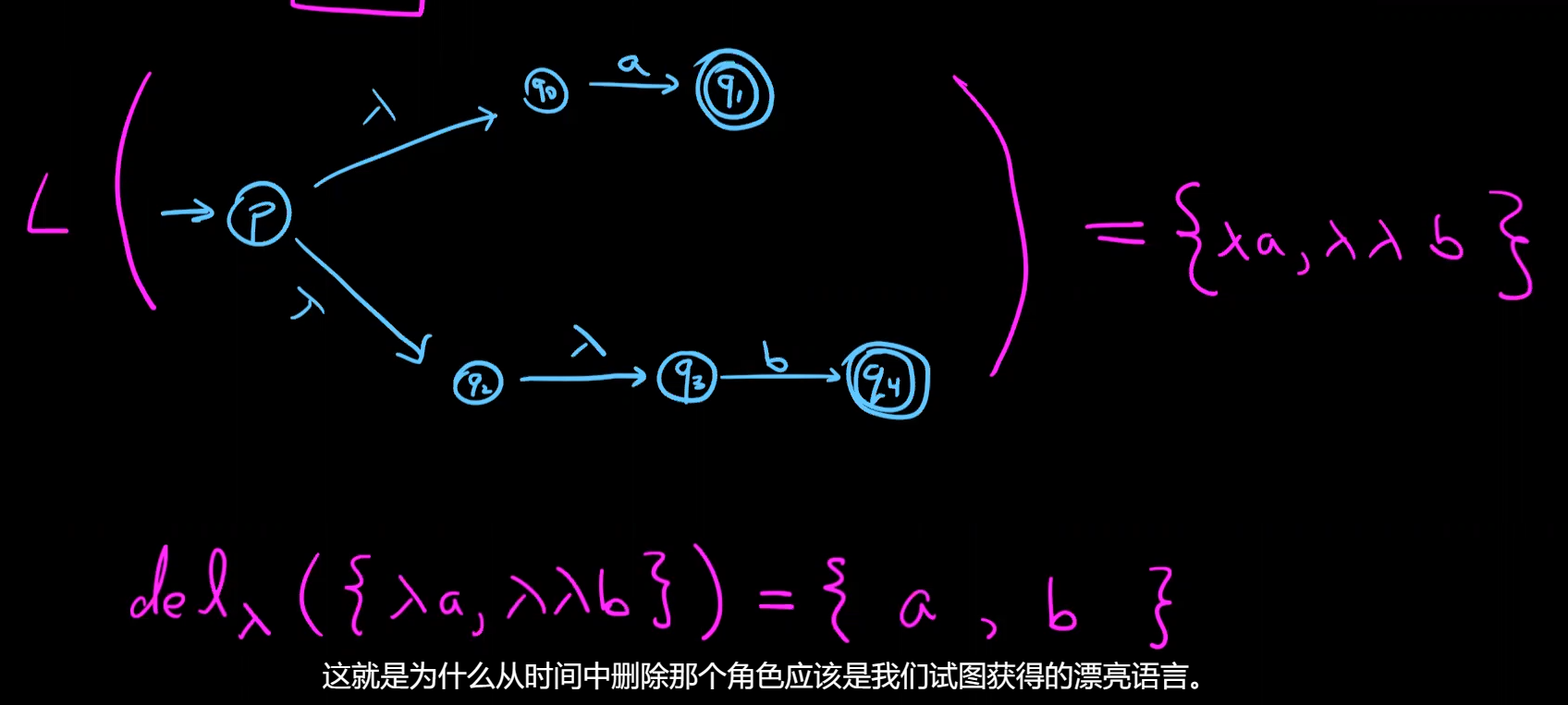
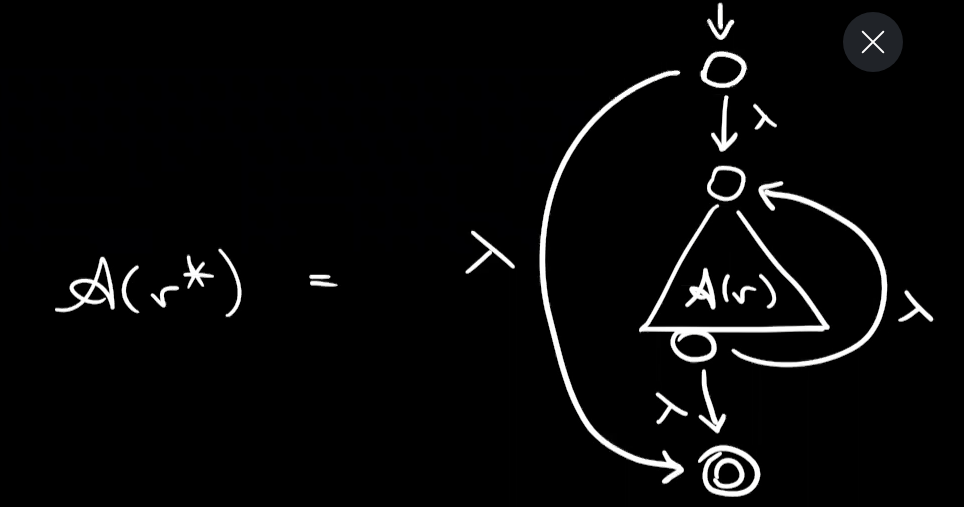
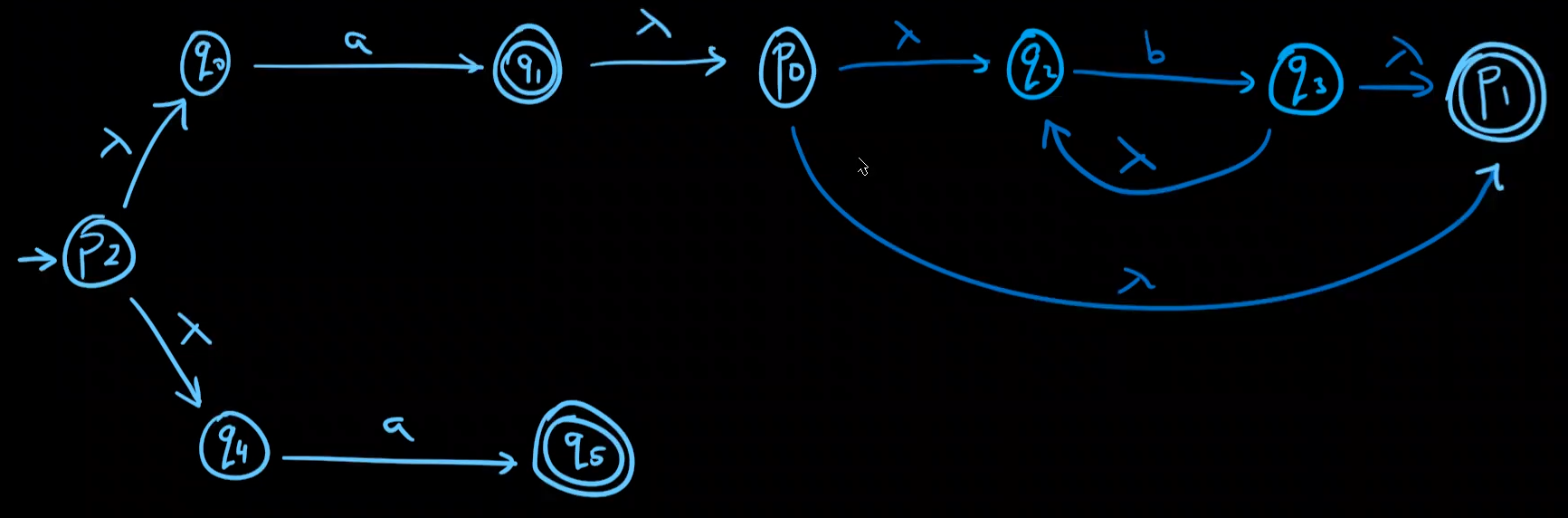
build $A(ab^*+a)$

DFA、NFA、NFA-λ相互转化
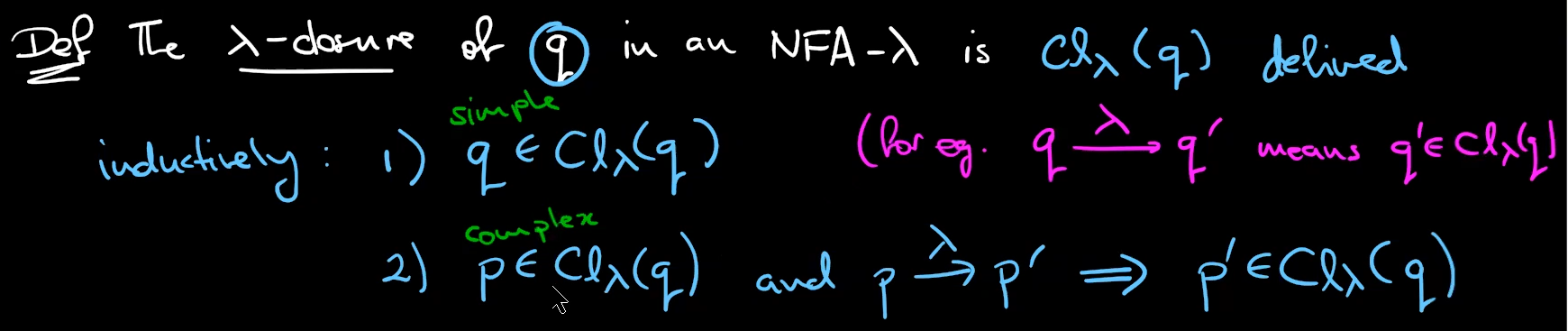

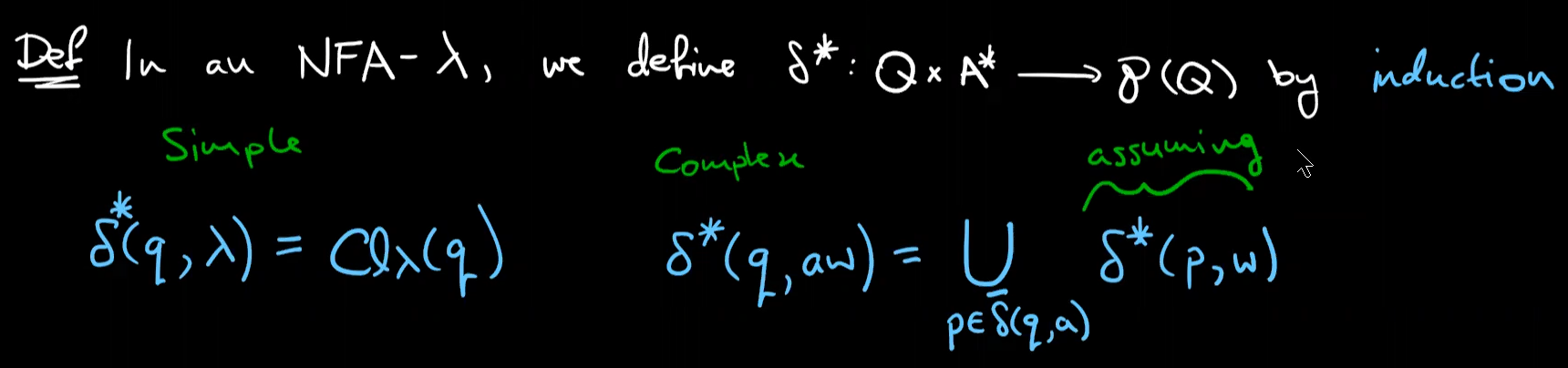
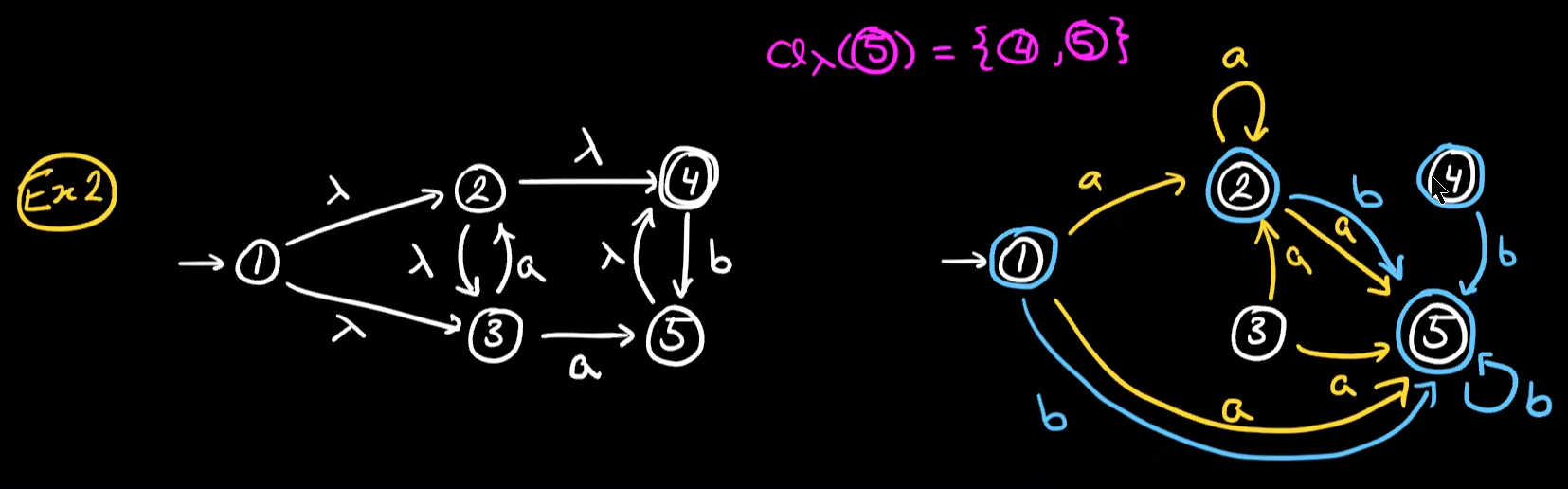
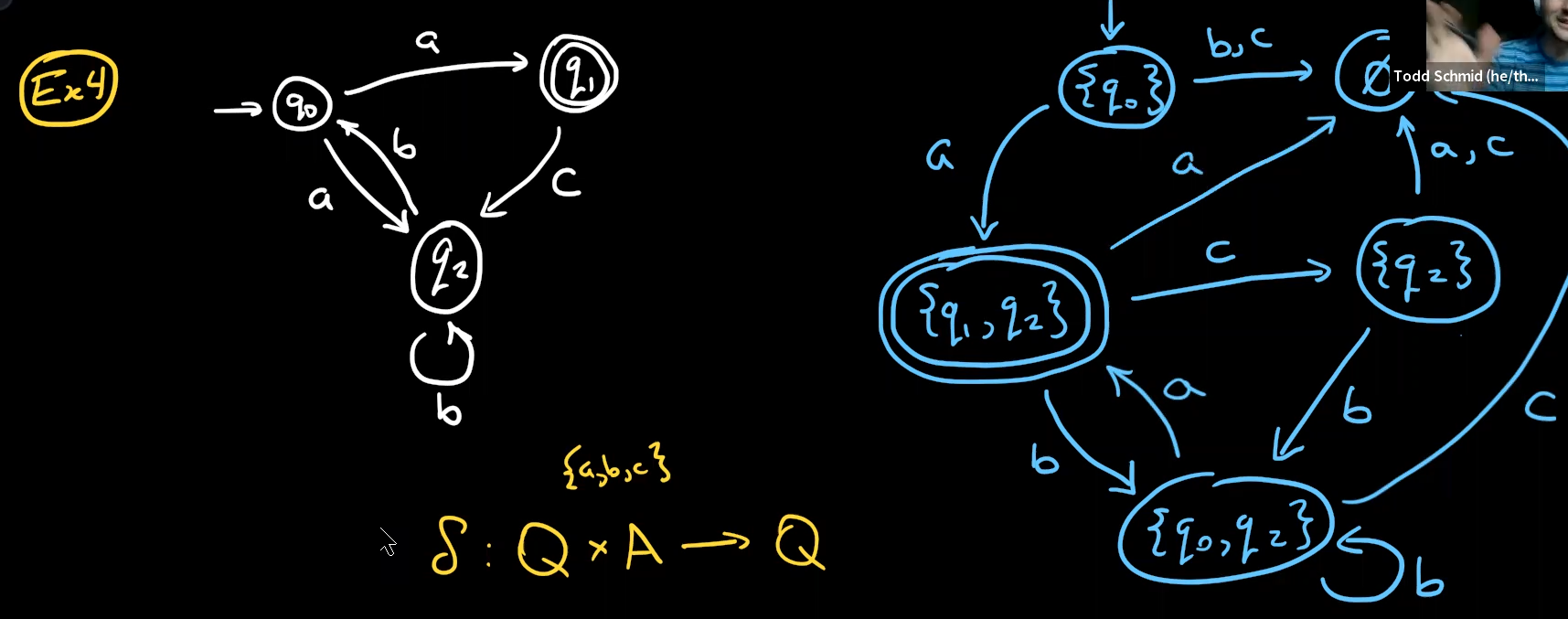
Kleene’s theorem
Regular expression -> NFA-λ -> NFA -> DFA转化
fact(*): if u,L,w are languages, λ不属于L, then if u=Lu+w, $u=L^ *w $
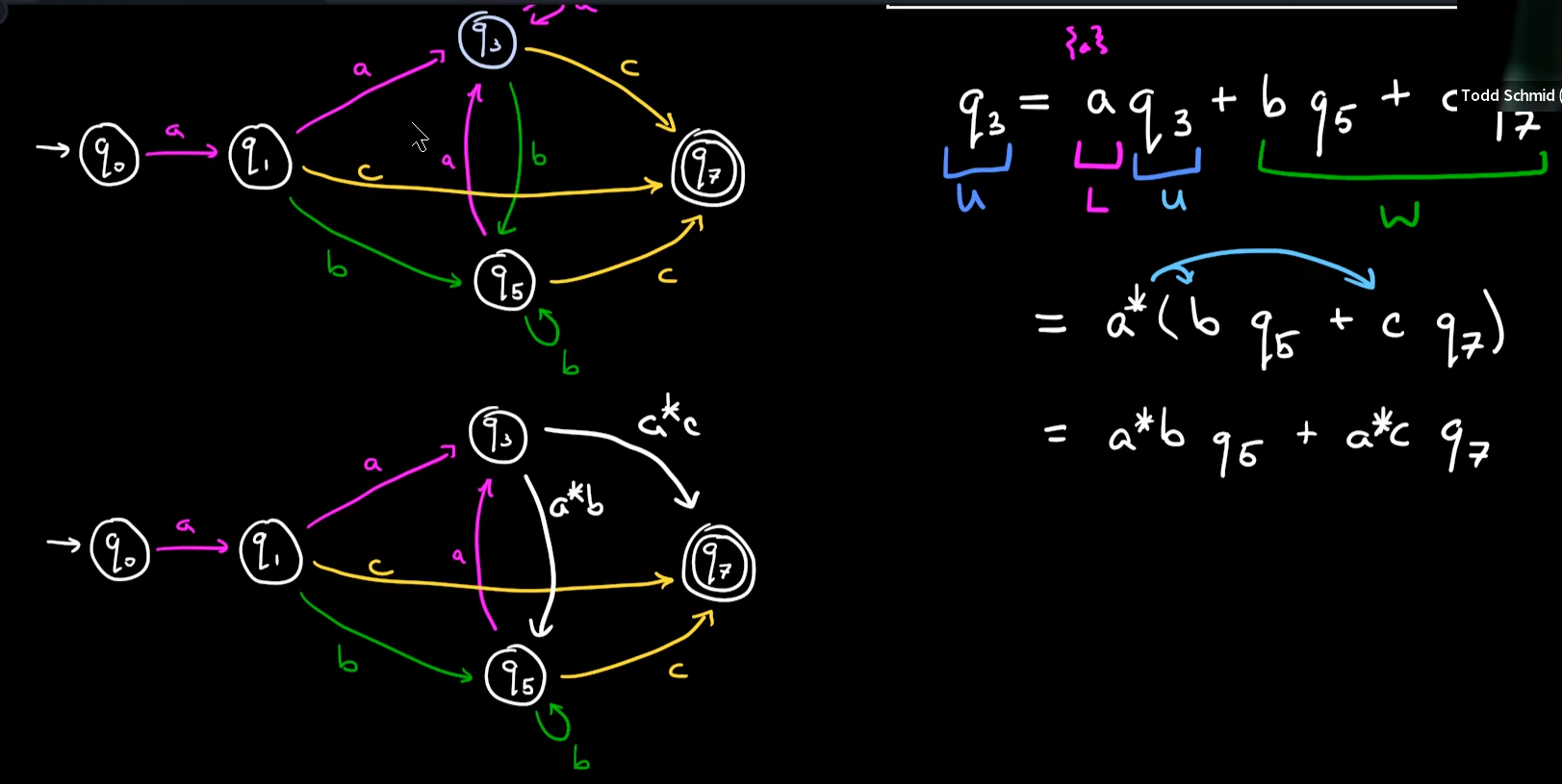
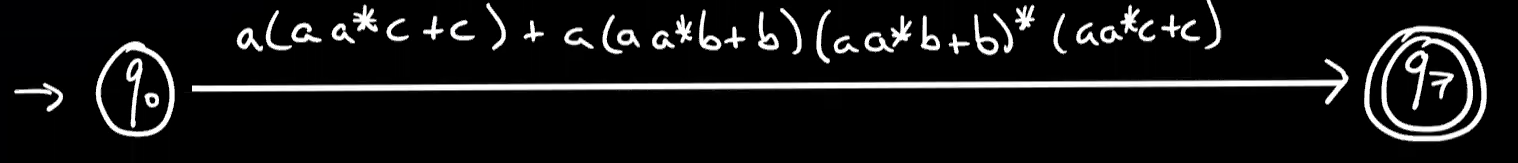
通过$aa^c+c=(aa^+1)c=a^*c$进行化简,对b同理
$a(a^c)+a(a^b)(a^b)^(a^c)=a((1+(a^b)(a^b)^)(a^c))=a(a^b)^a^c$
通过$(u^L)^u^*=(u+L)^*$进行化简得到$a(a+b)^*c$
R.exp.->DFA:Brzozowski Derivative
常规语言的闭包属性
Prove $A^*/L$ is a regular language
Main tool for showing closure properties: Kleene’s theorem
L is regular if L is recognized by a DFA
知识点:$w∈L^C$ if and only if w不属于L,表示补集
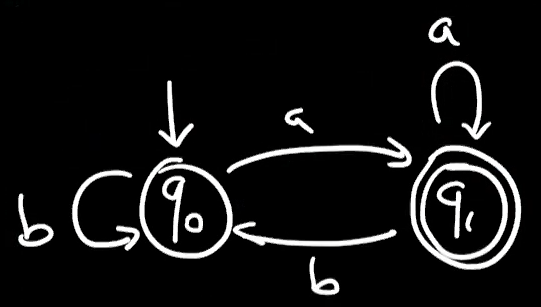
$b^a(a+bb^a)^*=b^a((1+bb^)a)^*=b^a(b^a)^*=(b^a)^b^a=(a+b)^a$
$[(a+b)^*]^c=?$
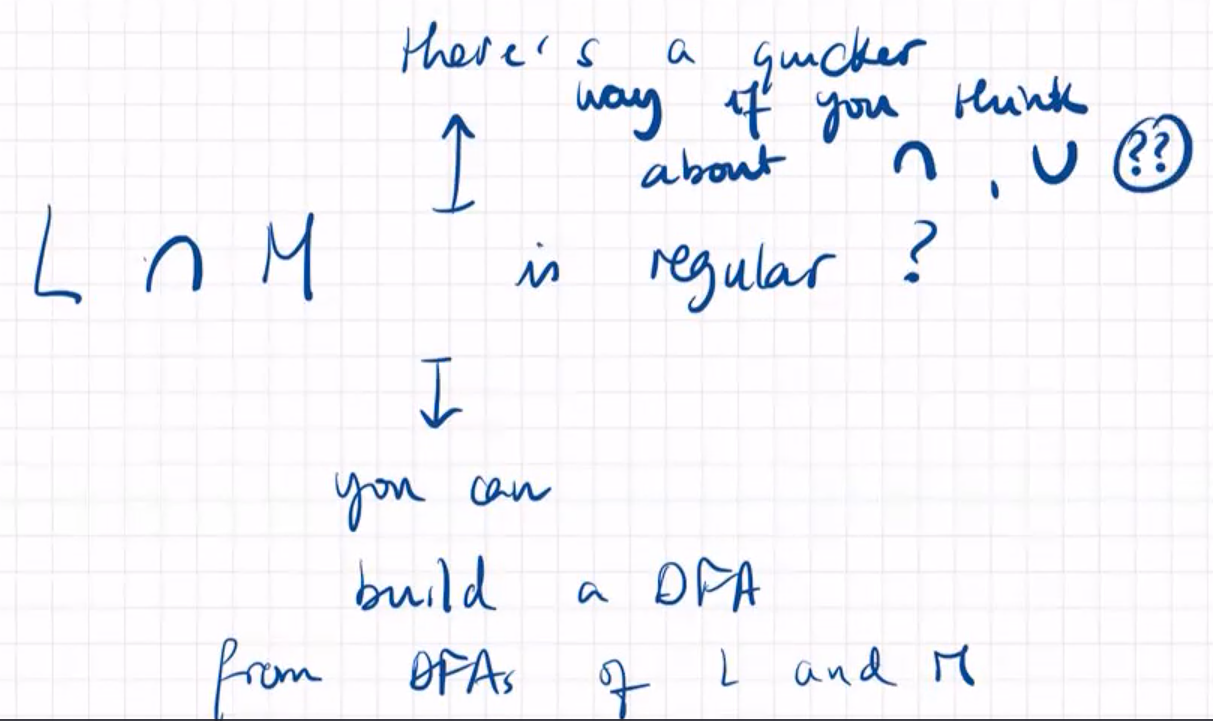
Fact: if $L_1$ and $L_2$ are regular languages, $L_1∩L_2$ is also regular.

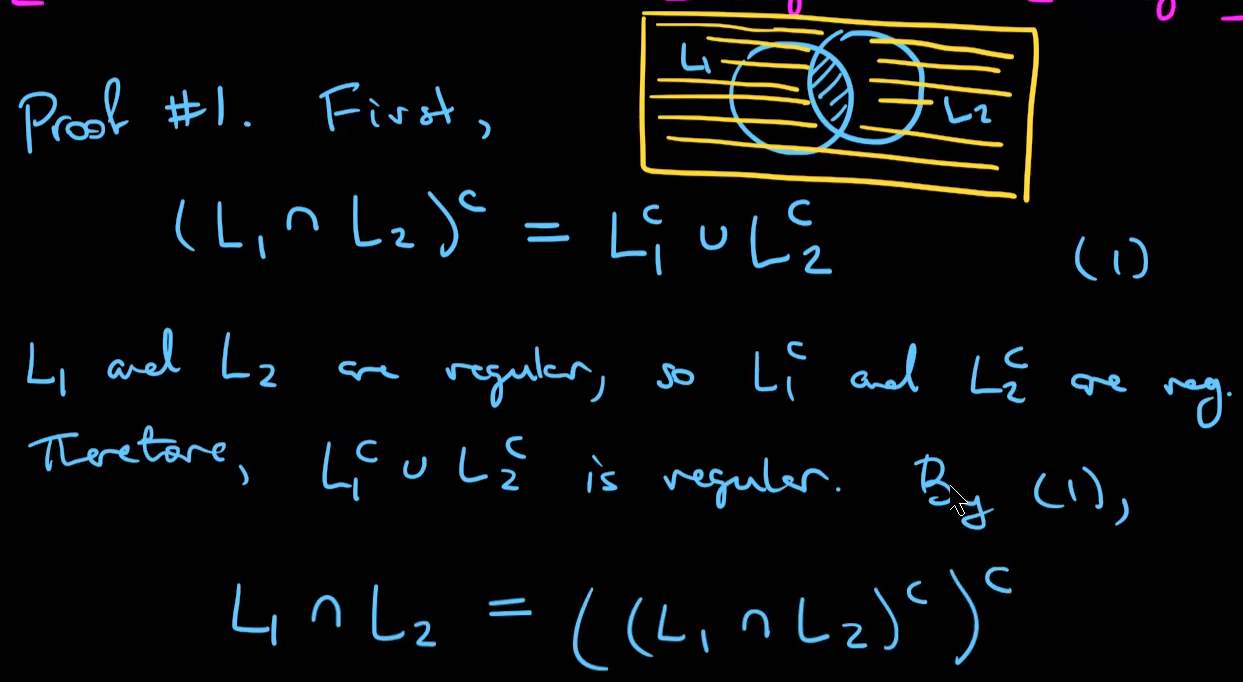
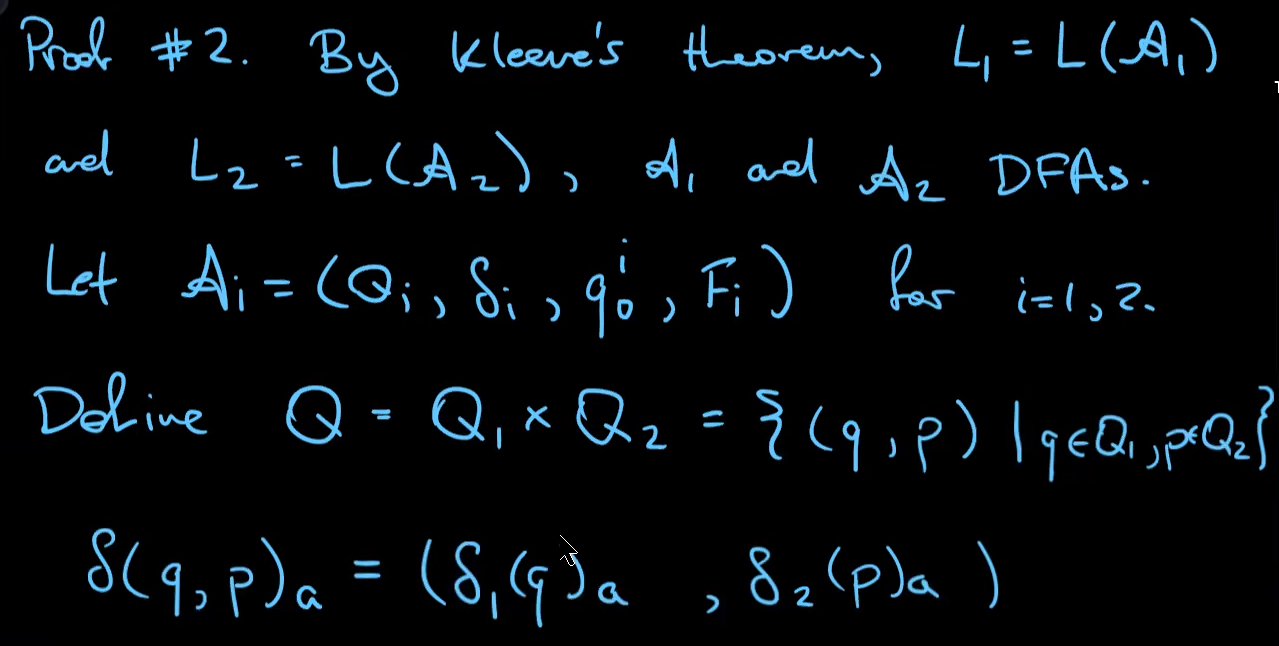
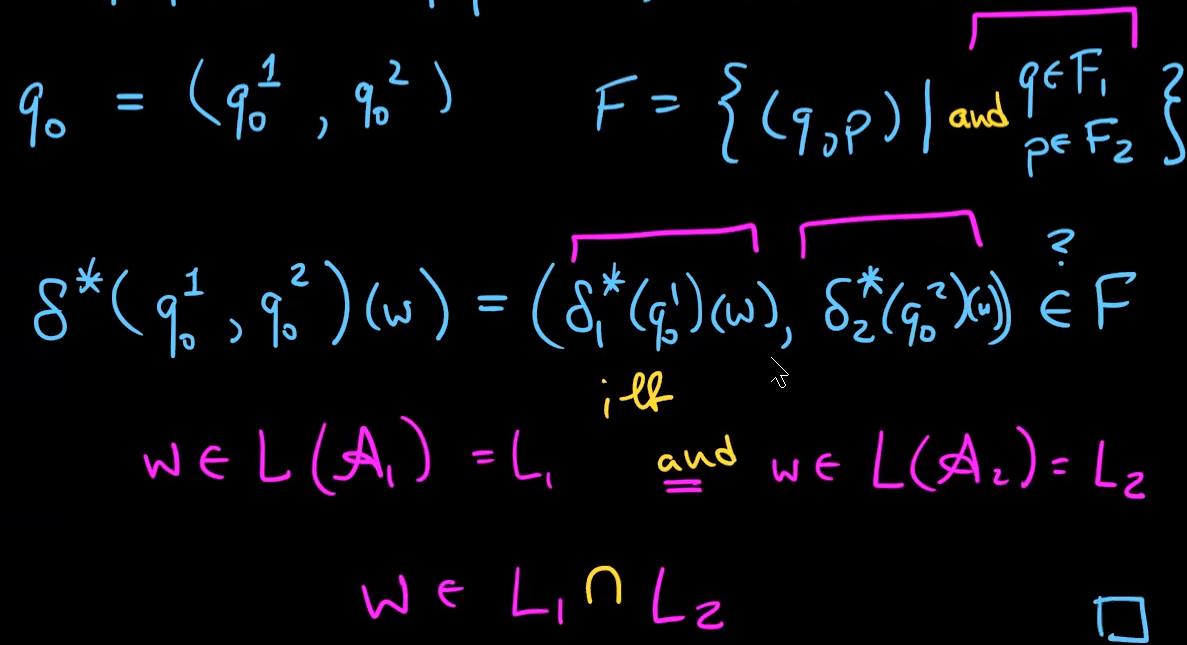
a language that is not regular

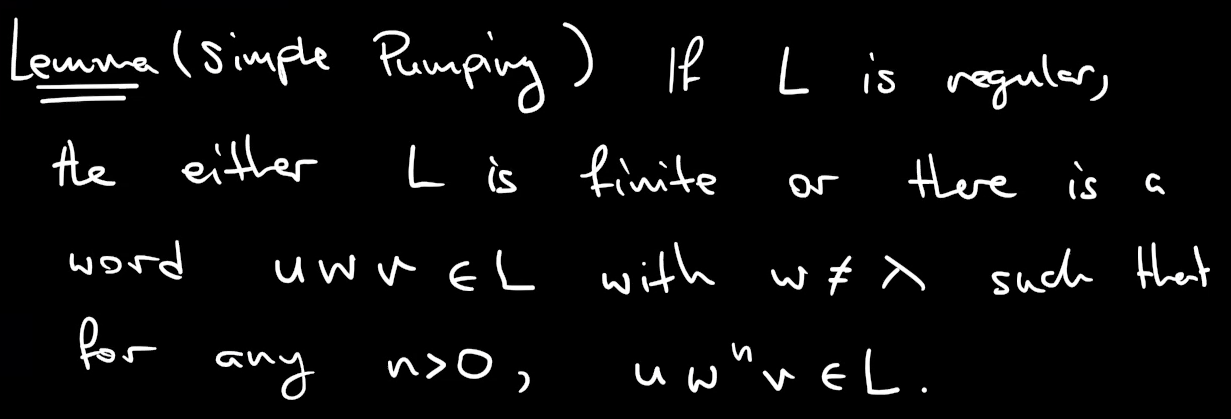
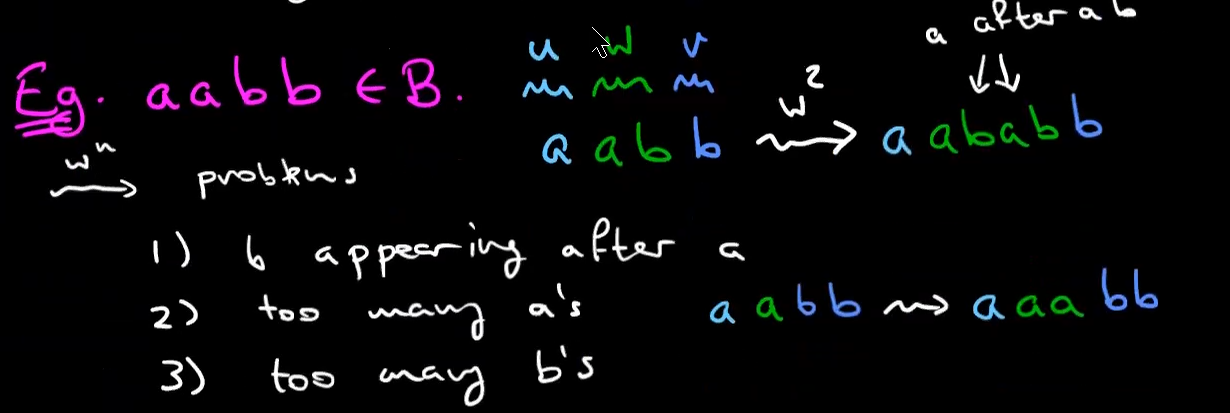
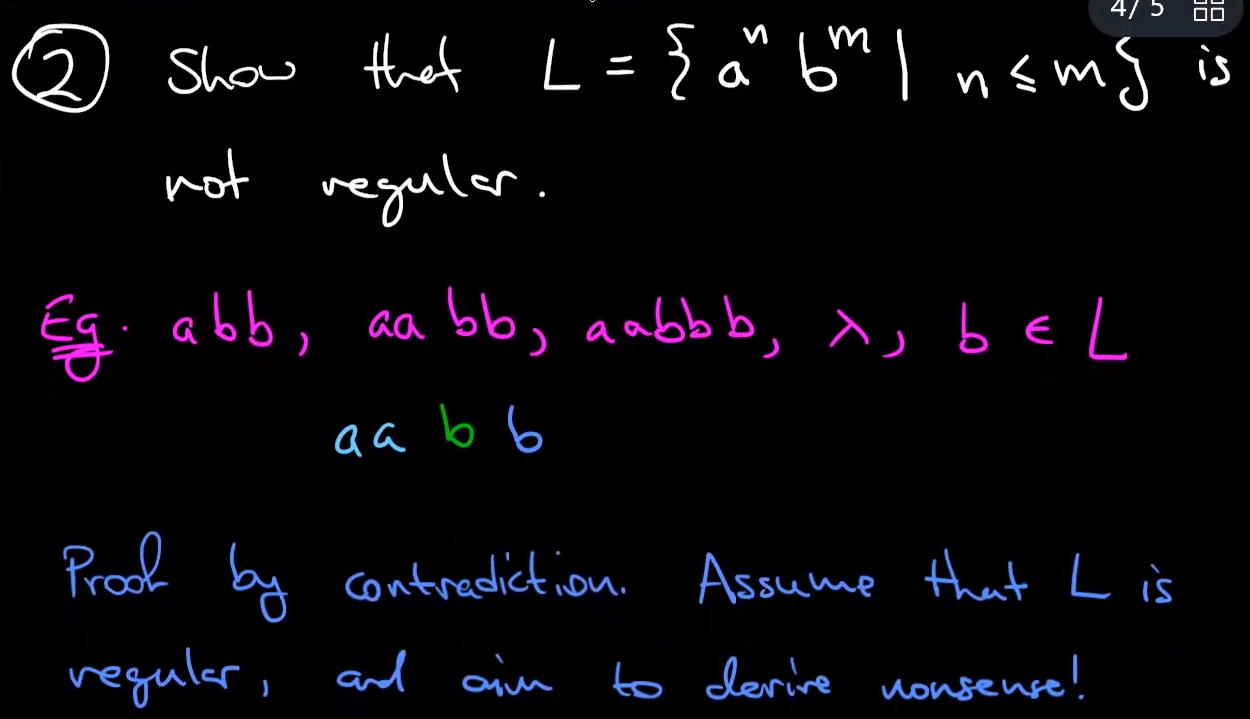
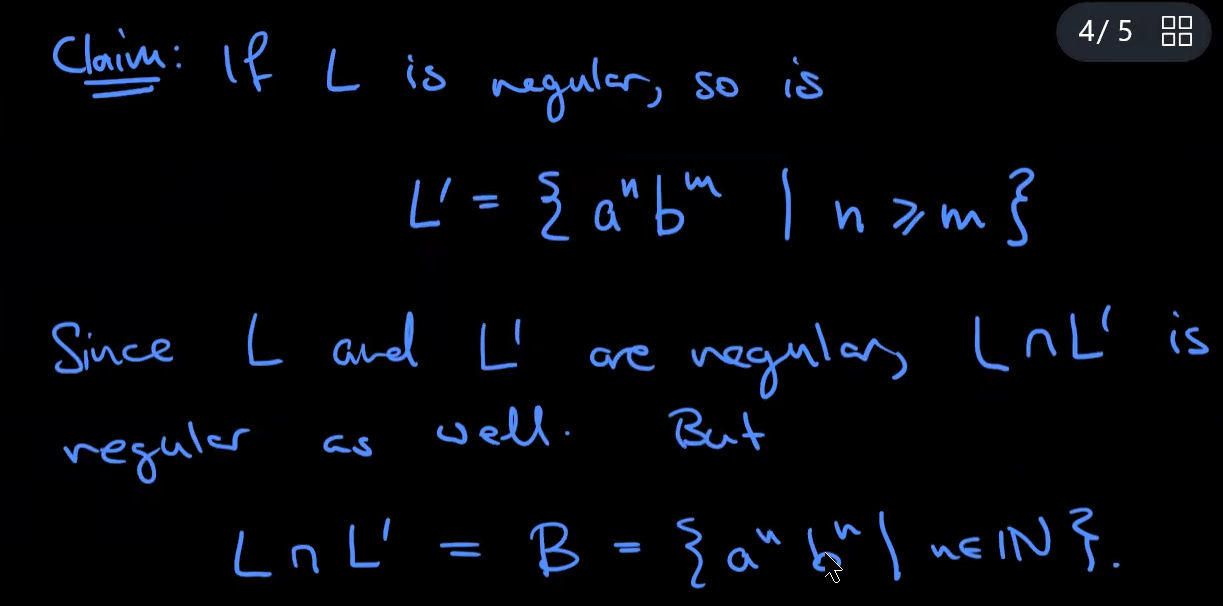
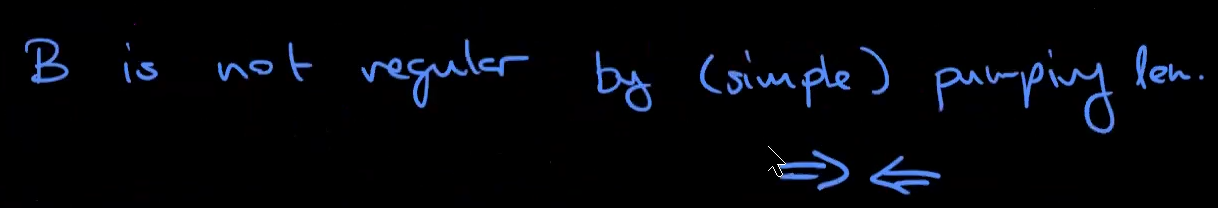
context free grammar
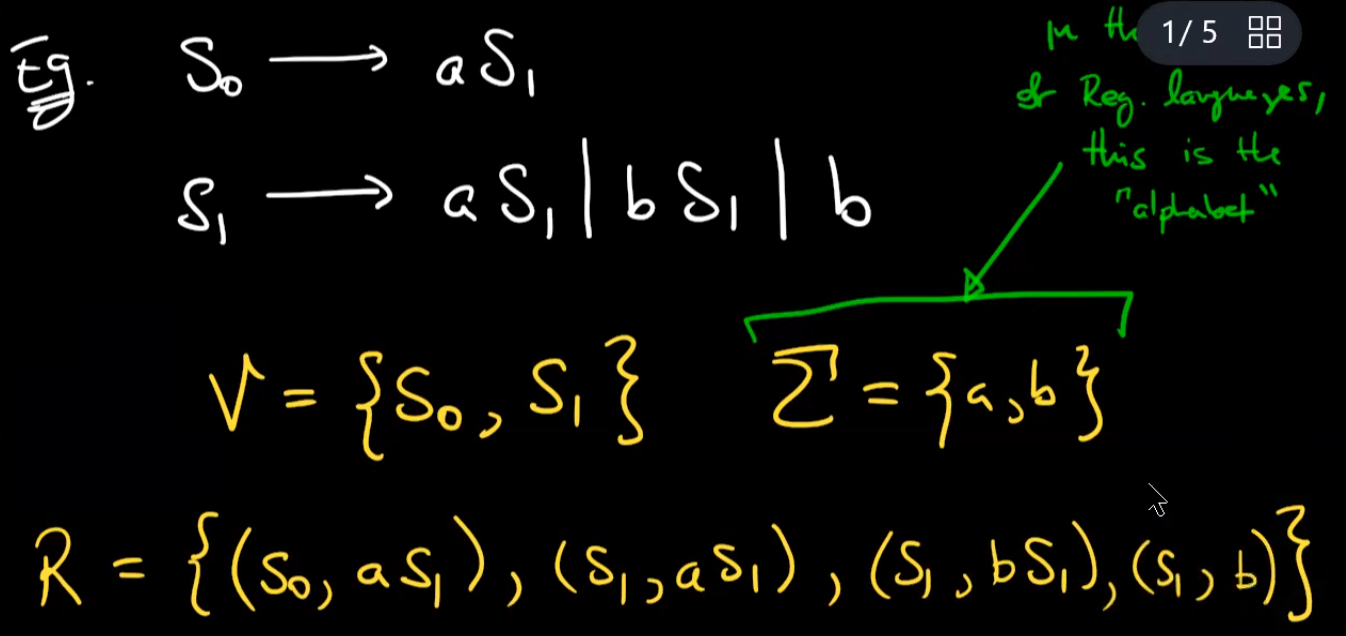

what language is generated by the CFG below?
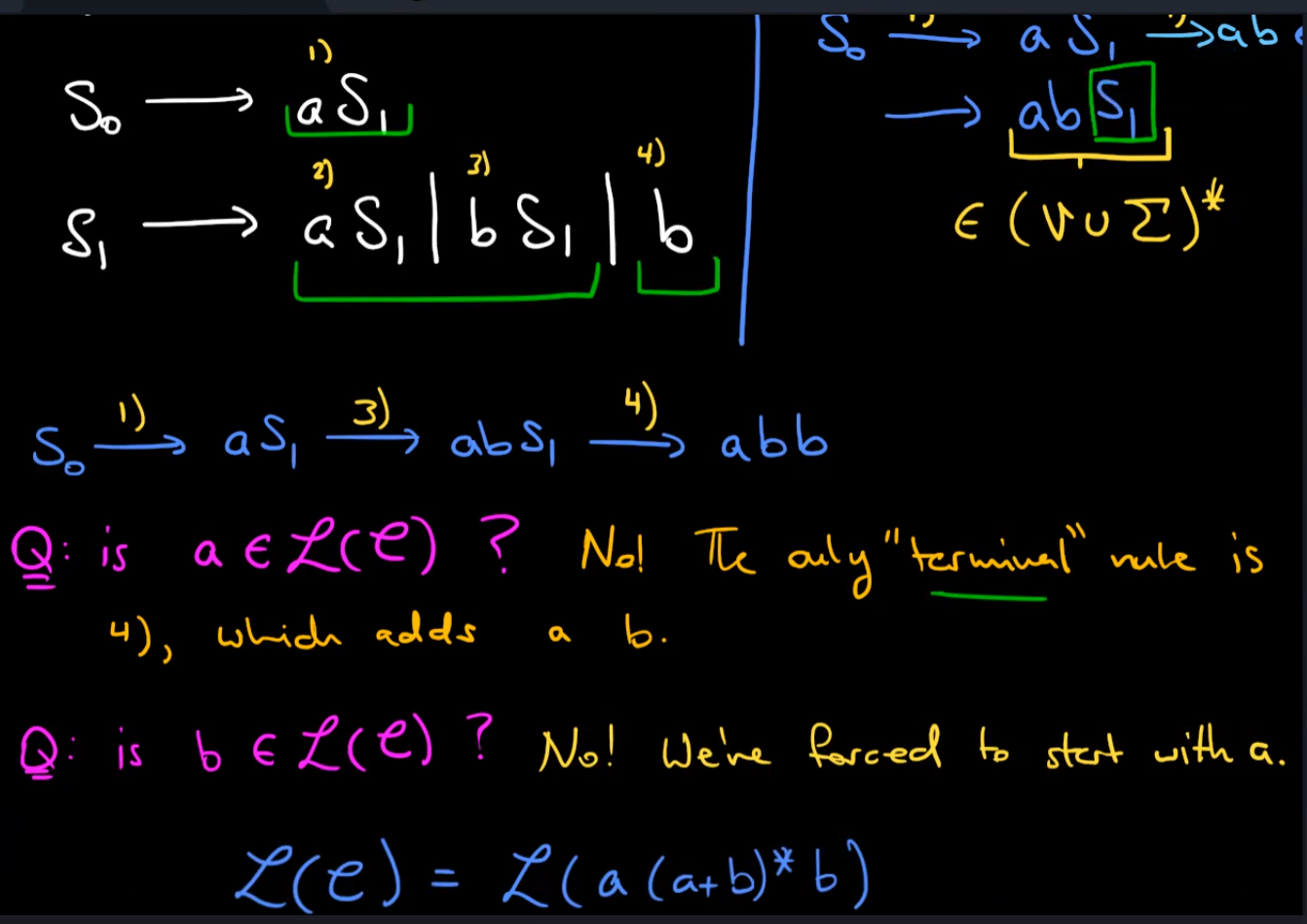
Design a CFG generating $L={0^n1^n|n>=0}∪{1^n0^n|n>=0} $
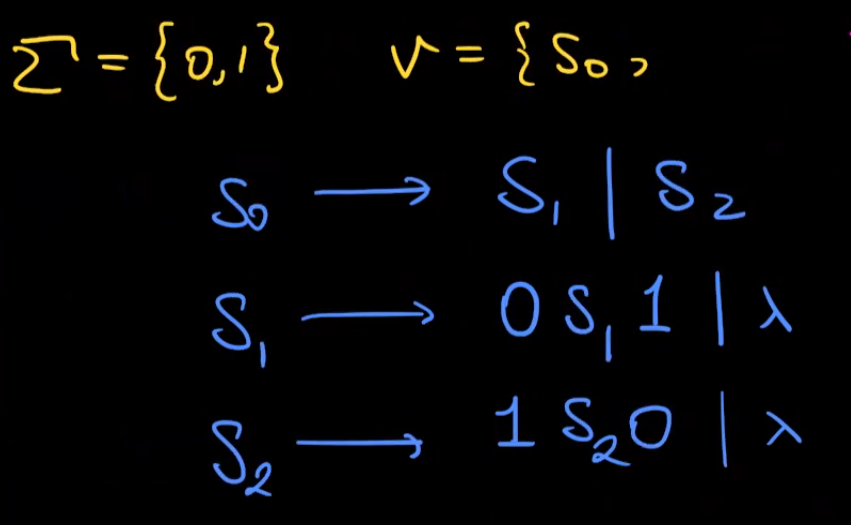

pushdown automata


another pumping lemma
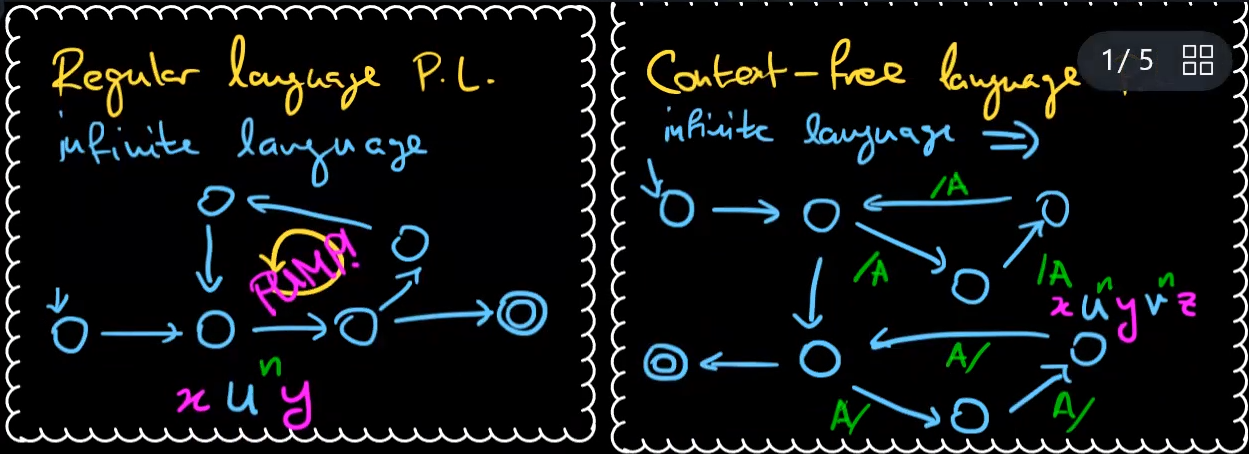
正则语言抽水定理:如果我有无限的正则语言,并且在自动机中曾经识别过,应该能够找到并使用一些循环来pump
上下文无关语言抽水定理:如果我有上下文无关语言,会在某一阶段多次将值推入堆栈上,并且在循环的稍后阶段将其多次弹出。

附言:学习link
编译原理学习之:正则表达式(regular expression)和非正则语言(non-regular languages)_暖仔会飞的博客-CSDN博客_编译原理正则表达式





