数据库任务二索引管理

任务2.1 B+树的查找 && 任务2.2 B+树的插入

任务要求

（1）结点内的查找

为了实现整个B+树的查找，首先需要实现B+树单个结点内部的查找。

class IxNodeHandle {
    // 结点内的查找
    int lower_bound(const char *target) const;
    int upper_bound(const char *target) const;
    bool LeafLookup(const char *key, Rid **value);
    page_id_t InternalLookup(const char *key);
}

（2）B+树的查找

class IxIndexHandle {
    // B+树的查找
    IxNodeHandle *FindLeafPage(const char *key, Operation operation, Transaction *transaction);
    bool GetValue(const char *key, std::vector<Rid> *result, Transaction *transaction);
}

（3）结点内的插入

class IxNodeHandle {
    // 结点内的插入
    void insert_pairs(int pos, const char *key, const Rid *rid, int n);
    int Insert(const char *key, const Rid &value);
}

（4）B+树的插入

class IxIndexHandle {
    // B+树的插入
    bool insert_entry(const char *key, const Rid &value, Transaction *transaction);
    IxNodeHandle *Split(IxNodeHandle *node);
    void InsertIntoParent(IxNodeHandle *old_node, const char *key, IxNodeHandle *new_node, Transaction *transaction);
}

通关截图

代码分析

（1）结点内的查找

ix_node_handle.cpp

lower_bound函数

/**
 * @brief 在当前node中查找第一个>=target的key_idx
 *
 * @return key_idx，范围为[0,num_key)，如果返回的key_idx=num_key，则表示target大于最后一个key
 * @note 返回key index（同时也是rid index），作为slot no
 */
int IxNodeHandle::lower_bound(const char *target) const {
    // Todo:
    // 查找当前节点中第一个大于等于target的key，并返回key的位置给上层
    // 提示: 可以采用多种查找方式，如顺序遍历、二分查找等；使用ix_compare()函数进行比较
    int x = 0;
    int end = page_hdr->num_key;
    int mid, flag;
	while(x < end){
		mid = (x + end) / 2;
		flag = ix_compare(get_key(mid), target, file_hdr->col_type, file_hdr->col_len);
		if(flag < 0){			
            x = mid + 1;
        }
		else{
			end = mid;
        }
	}
    return x;
}

采用二分查找，设定初始下限为x=0，初始上限为end=page_hdr->num_key，通过不断比较mid处value与target的值，不断收紧范围，直到x=end。由于当get_key(mid)<target 时总有x = mid + 1，直到满足条件或者所有value都比target小，即x=end=mid=page_hdr->num_key。

upper_bound函数

/**
 * @brief 在当前node中查找第一个>target的key_idx
 *
 * @return key_idx，范围为[1,num_key)，如果返回的key_idx=num_key，则表示target大于等于最后一个key
 * @note 注意此处的范围从1开始
 */
int IxNodeHandle::upper_bound(const char *target) const {
    // Todo:
    // 查找当前节点中第一个大于target的key，并返回key的位置给上层
    // 提示: 可以采用多种查找方式：顺序遍历、二分查找等；使用ix_compare()函数进行比较
    int x = 1;
    int end = page_hdr->num_key;
    int mid, flag;
    while(x < end){
        mid = (x + end) / 2;
        flag = ix_compare(get_key(mid), target, file_hdr->col_type, file_hdr->col_len);
        if(flag > 0){
            end = mid; 
        }
        else{
            x = mid + 1;
        }
    }
    return x;
}

采用二分查找，设定初始下限为x=1，初始上限为end=page_hdr->num_key，通过不断比较mid处value与target的值，不断收紧范围，直到x=end。由于当get_key(mid)<=target 时总有x = mid + 1，直到满足条件或者所有value都小于等于target，即x=end=mid=page_hdr->num_key。

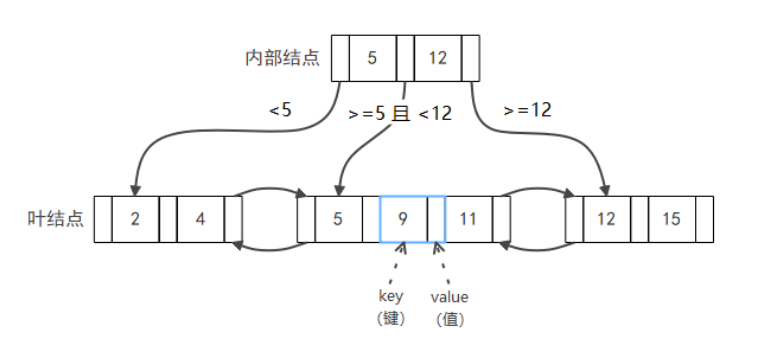
为什么初始上限为x=1而不是x=0，因为根据B+树的构造，为了使value的数量与key相等，于是在每个内部结点的第一个value前面额外加上第一个key，这就意味着第一个key存储的是以该结点为根结点的子树中的所有key的最小值，x上限为1则可以避免非叶结点受到影响。

LeafLookup函数

/**
 * @brief 用于叶子结点根据key来查找该结点中的键值对
 * 值value作为传出参数，函数返回是否查找成功
 *
 * @param key 目标key
 * @param[out] value 传出参数，目标key对应的Rid
 * @return 目标key是否存在
 */
bool IxNodeHandle::LeafLookup(const char *key, Rid **value) {
    // Todo:
    // 1. 在叶子节点中获取目标key所在位置
    // 2. 判断目标key是否存在
    // 3. 如果存在，获取key对应的Rid，并赋值给传出参数value
    // 提示：可以调用lower_bound()和get_rid()函数。
    int pos = lower_bound(key);
    if(ix_compare(get_key(pos), key, file_hdr->col_type, file_hdr->col_len) == 0){
		*value = get_rid(pos);
		return true;
	}
	else{
    	return false;
    }
}

首先使用lower_bound函数找到第一个满足大于等于key值的位置pos，并判断get_key(pos)和key是否相等。如果相等则说明key存在，使用get_rid获取key对应的rid。

InternalLookup函数

/**
 * 用于内部结点（非叶子节点）查找目标key所在的孩子结点（子树）
 * @param key 目标key
 * @return page_id_t 目标key所在的孩子节点（子树）的存储页面编号
 */
page_id_t IxNodeHandle::InternalLookup(const char *key) {
    // Todo:
    // 1. 查找当前非叶子节点中目标key所在孩子节点（子树）的位置
    // 2. 获取该孩子节点（子树）所在页面的编号
    // 3. 返回页面编号
    // int pos = lower_bound(key);
    // return ValueAt(pos); 
    int pos = upper_bound(key);
    return ValueAt(pos -1); 
}

要完成该函数，upper_bound函数

根据B+树的结构，当value位于key右边表示value>=key，value位于key左边表示value<key，upper_bound可以找到当前节点中第一个大于target的key的位置pos，由于key与value一一对应并且key在左value在右，所以直接pos-1就可以找到value所对应得key。而如果使用lower_bound函数，如果value大于key值，则与上面同理。但如果value值与key值相等，得到第一个大于target的key的位置pos并不是最终结果，所寻找的value归pos-1处得key管辖。
另一种情况如果value的值比以该结点为根结点的子树中的所有key的最小值还小，因为upper_bound的上限为1，抛开了最小值的影响，正确的找到了位于0处的value。但是lower_bound将该key考虑在内，得到了-1的pos，显然为错误的结果。位于0处的key只是作为最小值的表现形式，并不能将value进行分割。

下面是使用lower_bound的正确写法

int pos = lower_bound(key);
if(ix_compare(get_key(pos), key, file_hdr->col_type, file_hdr->col_len) == 0)
    return ValueAt(pos);
if ((pos-1)<0)  
    return ValueAt(pos);
return ValueAt(pos-1);

（2）B+树的查找

ix_index_handle.cpp

FindLeafPage函数

/**
 * @brief 用于查找指定键所在的叶子结点
 *
 * @param key 要查找的目标key值
 * @param operation 查找到目标键值对后要进行的操作类型
 * @param transaction 事务参数，如果不需要则默认传入nullptr
 * @return 返回目标叶子结点
 * @note need to Unpin the leaf node outside!
 */
IxNodeHandle *IxIndexHandle::FindLeafPage(const char *key, Operation operation, Transaction *transaction) {
    // Todo:
    // 1. 获取根节点
    // 2. 从根节点开始不断向下查找目标key
    // 3. 找到包含该key值的叶子结点停止查找，并返回叶子节点
    IxNodeHandle *node = FetchNode(file_hdr_.root_page);
    while(!node->page_hdr->is_leaf){
        buffer_pool_manager_->UnpinPage(node->GetPageId(), false);
        node = FetchNode(node->InternalLookup(key));
    };
    buffer_pool_manager_->UnpinPage(node->GetPageId(), false);  
    return node;
}

通过file_hdr_.root_page获取根页号，使用FetchNode函数通过页号得到节点指针。非叶子节点不断调用InternalLookup函数，查找目标key所在的孩子结点，直到到达叶节点，返回叶节点即可。

GetValue函数

/**
 * @brief 用于查找指定键在叶子结点中的对应的值result
 *
 * @param key 查找的目标key值
 * @param result 用于存放结果的容器
 * @param transaction 事务指针
 * @return bool 返回目标键值对是否存在
 */
bool IxIndexHandle::GetValue(const char *key, std::vector<Rid> *result, Transaction *transaction) {
    // Todo:
    // 1. 获取目标key值所在的叶子结点
    // 2. 在叶子节点中查找目标key值的位置，并读取key对应的rid
    // 3. 把rid存入result参数中
    // 提示：使用完buffer_pool提供的page之后，记得unpin page；记得处理并发的上锁
    std::scoped_lock lock{root_latch_};
	IxNodeHandle *leaf = FindLeafPage(key, Operation::FIND, transaction);
    Rid* rid = nullptr;
	buffer_pool_manager_->UnpinPage(leaf->GetPageId(), false);
	if(leaf->LeafLookup(key, &rid)){
		result->push_back(*rid);
		return true;
	}
	else
		return false;
}

找到目标key值所在的叶子结点，定义空Rid，用于存储传出的所求键值对值value，并返回是否操作成功。

（3）结点内的插入

ix_node_handle.cpp

insert_pairs函数

/**
 * @brief 在指定位置插入n个连续的键值对
 * 将key的前n位插入到原来keys中的pos位置；将rid的前n位插入到原来rids中的pos位置
 *
 * @param pos 要插入键值对的位置
 * @param (key, rid) 连续键值对的起始地址，也就是第一个键值对，可以通过(key, rid)来获取n个键值对
 * @param n 键值对数量
 * @note [0,pos)           [pos,num_key)
 *                            key_slot
 *                            /      \
 *                           /        \
 *       [0,pos)     [pos,pos+n)   [pos+n,num_key+n)
 *                      key           key_slot
 */
void IxNodeHandle::insert_pairs(int pos, const char *key, const Rid *rid, int n) {
    // Todo:
    // 1. 判断pos的合法性
    // 2. 通过key获取n个连续键值对的key值，并把n个key值插入到pos位置
    // 3. 通过rid获取n个连续键值对的rid值，并把n个rid值插入到pos位置
    // 4. 更新当前节点的键数量
    assert(pos >= 0 && pos <= page_hdr->num_key);
    int key_len = file_hdr->col_len;
    memmove(get_key(pos+n), get_key(pos), (page_hdr->num_key - pos) * key_len);
    memcpy(get_key(pos), key, n * key_len);
    memmove(get_rid(pos+n), get_rid(pos), (page_hdr->num_key - pos) * sizeof(Rid));
    memcpy(get_rid(pos), rid, n * sizeof(Rid));
    page_hdr->num_key += n;
}

使用assert断言pos的合法性，下面使用系统中的memmove和memcpy函数

memmove函数的声明如下

1	void memmove(void str1, const void *str2, size_t n)

参数：

str1 – 指向用于存储复制内容的目标数组，类型强制转换为 void* 指针。
str2 – 指向要复制的数据源，类型强制转换为 void* 指针。
n – 要被复制的字节数。

memcpy函数的声明如下

1	void memcpy(void str1, const void *str2, size_t n)

参数：

str1 – 指向用于存储复制内容的目标数组，类型强制转换为 void* 指针。
str2 – 指向要复制的数据源，类型强制转换为 void* 指针。
n – 要被复制的字节数。

插入的过程是首先将pos至page_hdr->num_key处，共(page_hdr->num_key - pos)*size大小的内容向后移动n个位置，即搬到pos+n位置处。其中key的size为file_hdr->col_len，value的size为sizeof(Rid)。

insert函数

/**
 * @brief 用于在结点中插入单个键值对。
 * 函数返回插入后的键值对数量
 *
 * @param (key, value) 要插入的键值对
 * @return int 键值对数量
 */
int IxNodeHandle::Insert(const char *key, const Rid &value) {
    // Todo:
    // 1. 查找要插入的键值对应该插入到当前节点的哪个位置
    // 2. 如果key重复则不插入
    // 3. 如果key不重复则插入键值对
    // 4. 返回完成插入操作之后的键值对数量
    int pos = lower_bound(key);
    if(ix_compare(get_key(pos), key, file_hdr->col_type, file_hdr->col_len) != 0){
        insert_pair(pos, key, value);
        return GetSize();     
    }
    else{
        return -1;
    }
}

找到位置，判断是否重复，重复返回-1，不重复返回键值对数量。

（4）B+树的插入

ix_index_handle.cpp

insert_entry函数

/**
 * @brief 将指定键值对插入到B+树中
 *
 * @param (key, value) 要插入的键值对
 * @param transaction 事务指针
 * @return 是否插入成功
 */
bool IxIndexHandle::insert_entry(const char *key, const Rid &value, Transaction *transaction) {
    // Todo:
    // 1. 查找key值应该插入到哪个叶子节点
    // 2. 在该叶子节点中插入键值对
    // 3. 如果结点已满，分裂结点，并把新结点的相关信息插入父节点
    // 提示：记得unpin page；若当前叶子节点是最右叶子节点，则需要更新file_hdr_.last_leaf；记得处理并发的上锁
    std::scoped_lock lock{root_latch_};
    IxNodeHandle *leaf = FindLeafPage(key, Operation::INSERT, transaction);
    if(leaf->Insert(key, value) == -1){
        buffer_pool_manager_->UnpinPage(leaf->GetPageId(), false);	
		return false;
    }
    else if(leaf->GetSize() == leaf->GetMaxSize()){
        IxNodeHandle *new_leaf = Split(leaf);
        if(leaf->GetPageNo() == file_hdr_.last_leaf){
            file_hdr_.last_leaf = new_leaf->GetPageNo();
        }
        InsertIntoParent(leaf, new_leaf->get_key(0), new_leaf, transaction);
        buffer_pool_manager_->UnpinPage(new_leaf->GetPageId(), true);
    }
    buffer_pool_manager_->UnpinPage(leaf->GetPageId(), false);
    return true;
}

根据key值找到应该插入的叶节点，执行插入操作，如果插入失败（重复）则未操作返回false，插入成功后对结点数量判断，如果满则调用split函数。由于B+树结构，需要将新节点的第一个key值插入父节点。若当前叶子节点是最右叶子节点，则需要更新file_hdr_.last_leaf。

split函数

/**
 * @brief 将传入的一个node拆分(Split)成两个结点，在node的右边生成一个新结点new node
 *
 * @param node 需要拆分的结点
 * @return 拆分得到的new_node
 * @note 本函数执行完毕后，原node和new node都需要在函数外面进行unpin
 */
IxNodeHandle *IxIndexHandle::Split(IxNodeHandle *node) {
    // Todo:
    // 1. 将原结点的键值对平均分配，右半部分分裂为新的右兄弟结点
    //    需要初始化新节点的page_hdr内容
    // 2. 如果新的右兄弟结点是叶子结点，更新新旧节点的prev_leaf和next_leaf指针
    //    为新节点分配键值对，更新旧节点的键值对数记录
    // 3. 如果新的右兄弟结点不是叶子结点，更新该结点的所有孩子结点的父节点信息(使用    		IxNodeHandle *new_node = CreateNode();
    new_node->page_hdr->num_key = 0;
    new_node->page_hdr->next_free_page_no = node->page_hdr->next_free_page_no;
    new_node->page_hdr->parent = node->GetParentPageNo();
    bool judge_leaf = node->page_hdr->is_leaf;
    new_node->page_hdr->is_leaf = judge_leaf;
    if(judge_leaf){
        new_node->page_hdr->next_leaf = node->page_hdr->next_leaf;
        new_node->page_hdr->prev_leaf = node->GetPageNo();
        node->page_hdr->next_leaf = new_node->GetPageNo();
        IxNodeHandle* next_node = FetchNode(new_node->page_hdr->next_leaf);
        next_node->page_hdr->prev_leaf = new_node->GetPageNo();
		buffer_pool_manager_->UnpinPage(next_node->GetPageId(), true);
    }
    int mid = node->page_hdr->num_key / 2;
    new_node->insert_pairs(0, node->get_key(mid), node->get_rid(mid), node->page_hdr->num_key - mid);
    node->page_hdr->num_key = mid;
    if(!judge_leaf){    
        for(int i = 0; i < new_node->page_hdr->num_key; i++){
            maintain_child(new_node, i);
        }
    }       
    return new_node;
}

首先将原结点的键值对平均分配，右半部分分裂为新的右兄弟结点，对新节点的page_hdr内容进行初始化。下面对节点是否为叶子节点进行讨论。

如果右兄弟结点是叶子结点，更新新旧节点的prev_leaf和next_leaf指针为新节点分配键值对，更新旧节点的键值对数记录。而非叶子节点没有前置叶节点和后置叶结点，所以可以略去。

如果新的右兄弟结点不是叶子结点，则其存在孩子节点，需要更新该结点的所有孩子结点的父节点信息。

InsertIntoParent函数

/**
 * @brief Insert key & value pair into internal page after split
 * 拆分(Split)后，向上找到old_node的父结点
 * 将new_node的第一个key插入到父结点，其位置在 父结点指向old_node的孩子指针 之后
 * 如果插入后>=maxsize，则必须继续拆分父结点，然后在其父结点的父结点再插入，即需要递归
 * 直到找到的old_node为根结点时，结束递归（此时将会新建一个根R，关键字为key，old_node和new_node为其孩子）
 *
 * @param (old_node, new_node) 原结点为old_node，old_node被分裂之后产生了新的右兄弟结点new_node
 * @param key 要插入parent的key
 * @note 一个结点插入了键值对之后需要分裂，分裂后左半部分的键值对保留在原结点，在参数中称为old_node，
 * 右半部分的键值对分裂为新的右兄弟节点，在参数中称为new_node（参考Split函数来理解old_node和new_node）
 * @note 本函数执行完毕后，new node和old node都需要在函数外面进行unpin
 */
void IxIndexHandle::InsertIntoParent(IxNodeHandle *old_node, const char *key, IxNodeHandle *new_node,
                                     Transaction *transaction) {
    // Todo:
    // 1. 分裂前的结点（原结点, old_node）是否为根结点，如果为根结点需要分配新的root
    // 2. 获取原结点（old_node）的父亲结点
    // 3. 获取key对应的rid，并将(key, rid)插入到父亲结点
    // 4. 如果父亲结点仍需要继续分裂，则进行递归插入
    // 提示：记得unpin page
    if(old_node->IsRootPage()){
        IxNodeHandle *new_root = CreateNode();
        new_root->page_hdr->is_leaf = 0;
        new_root->page_hdr->num_key = 0;
        new_root->page_hdr->parent = INVALID_PAGE_ID;
        new_root->page_hdr->next_free_page_no = IX_NO_PAGE;
        new_root->insert_pair(0, old_node->get_key(0), (Rid){old_node->GetPageNo(), -1});
        new_root->insert_pair(1, key, (Rid){new_node->GetPageNo(), -1});
        int new_root_page = new_root->GetPageNo();
		file_hdr_.root_page = new_root_page;
		new_node->page_hdr->parent = new_root_page;
		old_node->page_hdr->parent = new_root_page;
    }
    else{
        IxNodeHandle *parent_node = FetchNode(old_node->page_hdr->parent);
        parent_node->insert_pair(parent_node->find_child(old_node) + 1, key, (Rid){new_node->GetPageId().page_no, -1});
        if(parent_node->page_hdr->num_key == parent_node->GetMaxSize()){
            IxNodeHandle *new_parent_node = Split(parent_node);
            InsertIntoParent(parent_node, new_parent_node->get_key(0), new_parent_node, transaction);
            buffer_pool_manager_->UnpinPage(new_parent_node->GetPageId(), true);
        }
        buffer_pool_manager_->UnpinPage(parent_node->GetPageId(), true);
    }
}

首先判断旧节点是不是根节点，如果是根节点则分裂后需要指向一个新的根节点，并且需要进行根节点的初始化工作，B+树的深度加深一层。如果不是根节点则找到父节点进行插入，如果父节点也满了那就循环递归。

parent_node->insert_pair(parent_node->find_child(old_node) + 1, key, (Rid){new_node->GetPageId().page_no, -1});此处是将新节点的0key插入父节点，需要找到父节点中旧节点的位置pos，pos+1处才为新节点的位置。

任务2.3 B+树的删除

任务要求

（1）结点内的删除

class IxNodeHandle {
    // 结点内的删除
    void erase_pair(int pos);
    int Remove(const char *key);
}

（2）B+树的删除

class IxIndexHandle {
    // B+树的删除
    void delete_entry(const char *key, Transaction *transaction);
    bool CoalesceOrRedistribute(IxNodeHandle *node, Transaction *transaction);
    bool Coalesce(IxNodeHandle **neighbor_node, IxNodeHandle **node, IxNodeHandle **parent, int index, Transaction *transaction);
    void Redistribute(IxNodeHandle *neighbor_node, IxNodeHandle *node, IxNodeHandle *parent, int index);
    bool AdjustRoot(IxNodeHandle *old_root_node);
}

通关截图

代码分析

（1）结点内的删除

ix_node_handle.cpp

erase_pair函数

/**
 * @brief 用于在结点中的指定位置删除单个键值对
 *
 * @param pos 要删除键值对的位置
 */
void IxNodeHandle::erase_pair(int pos) {
    // Todo:
    // 1. 删除该位置的key
    // 2. 删除该位置的rid
    // 3. 更新结点的键值对数量
    memmove(get_key(pos), get_key(pos + 1), (page_hdr->num_key - pos - 1) * file_hdr->col_len);
    memmove(get_rid(pos), get_rid(pos + 1), (page_hdr->num_key - pos - 1) * sizeof(Rid));
    page_hdr->num_key --;
}

pos+1及后面的记录向前移动一个位置，覆盖掉pos处需要删除的记录

remove函数

/**
 * @brief 用于在结点中删除指定key的键值对。函数返回删除后的键值对数量
 *
 * @param key 要删除的键值对key值
 * @return 完成删除操作后的键值对数量
 */
int IxNodeHandle::Remove(const char *key) {
    // Todo:
    // 1. 查找要删除键值对的位置
    // 2. 如果要删除的键值对存在，删除键值对
    // 3. 返回完成删除操作后的键值对数量
    int pos = lower_bound(key);
    if(ix_compare(key, get_key(pos), file_hdr->col_type, file_hdr->col_len) == 0){
        erase_pair(pos);
        return page_hdr->num_key;
    }
    else{
        return -1;
    }
}

找到第一个大于等于的节点，判断是否相等。如果不相等则说明删除项不存在，返回-1。如果相等则调用erase_pair进行删除操作。

（2）B+树的删除

ix_index_handle.cpp

delete_entry函数

/**
 * @brief 用于删除B+树中含有指定key的键值对
 *
 * @param key 要删除的key值
 * @param transaction 事务指针
 * @return 是否删除成功
 */
bool IxIndexHandle::delete_entry(const char *key, Transaction *transaction) {
    // Todo:
    // 1. 获取该键值对所在的叶子结点
    // 2. 在该叶子结点中删除键值对
    // 3. 如果删除成功需要调用CoalesceOrRedistribute来进行合并或重分配操作，并根据函数返回结果判断是否有结点需要删除
    // 4. 如果需要并发，并且需要删除叶子结点，则需要在事务的delete_page_set中添加删除结点的对应页面；记得处理并发的上锁
    std::scoped_lock lock{root_latch_};
    IxNodeHandle *leaf = FindLeafPage(key, Operation::DELETE, transaction);
    if(leaf->Remove(key) != -1){
        CoalesceOrRedistribute(leaf, transaction);
        buffer_pool_manager_->UnpinPage(leaf->GetPageId(), true);
        return true;	
    }
    else{
        buffer_pool_manager_->UnpinPage(leaf->GetPageId(), false);	
        return false;
    }
}

获取key值对应的叶节点，调用remove函数删除，如果删除失败，则返回false，删除成功就调用CoalesceOrRedistribute函数来进行合并或重分配操作，并返回true；

CoalesceOrRedistribute函数

/**
 * @brief 用于处理合并和重分配的逻辑，用于删除键值对后调用
 *
 * @param node 执行完删除操作的结点
 * @param transaction 事务指针
 * @param root_is_latched 传出参数：根节点是否上锁，用于并发操作
 * @return 是否需要删除结点
 * @note User needs to first find the sibling of input page.
 * If sibling's size + input page's size >= 2 * page's minsize, then redistribute.
 * Otherwise, merge(Coalesce).
 */
bool IxIndexHandle::CoalesceOrRedistribute(IxNodeHandle *node, Transaction *transaction) {
    // Todo:
    // 1. 判断node结点是否为根节点
    //    1.1 如果是根节点，需要调用AdjustRoot() 函数来进行处理，返回根节点是否需要被删除
    //    1.2 如果不是根节点，并且不需要执行合并或重分配操作，则直接返回false，否则执行2
    // 2. 获取node结点的父亲结点
    // 3. 寻找node结点的兄弟结点（优先选取前驱结点）
    // 4. 如果node结点和兄弟结点的键值对数量之和，能够支撑两个B+树结点（即node.size+neighbor.size >=
    // NodeMinSize*2)，则只需要重新分配键值对（调用Redistribute函数）
    // 5. 如果不满足上述条件，则需要合并两个结点，将右边的结点合并到左边的结点（调用Coalesce函数）
    if(node->IsRootPage()){
        return AdjustRoot(node);
    }
    else{
        IxNodeHandle *parent_node = FetchNode(node->GetParentPageNo());
        int pos = parent_node->find_child(node);
        IxNodeHandle *brother_node = pos != 0 ? FetchNode(node->GetPrevLeaf()) : FetchNode(node->GetNextLeaf());
        if(node->GetSize() + brother_node->GetSize() >= node->GetMinSize() * 2){
            Redistribute(brother_node, node, parent_node, pos);
            buffer_pool_manager_->UnpinPage(parent_node->GetPageId(), true);
    	    buffer_pool_manager_->UnpinPage(brother_node->GetPageId(), true);
		    return false;
        }
        else{
            Coalesce(&brother_node, &node, &parent_node, pos, transaction);
            buffer_pool_manager_->UnpinPage(parent_node->GetPageId(), true);
    	    buffer_pool_manager_->UnpinPage(brother_node->GetPageId(), true);
		    return true;
        }
    }
    return false;
}

如果node节点是根节点，则调用adjustroot函数。如果不是根节点，获取父节点和兄弟节点。其中如果node处于0处，没有前置节点，则取后置节点，其余pos取前置节点。如果node结点和兄弟结点的键值对数量之和，能够支撑两个B+树结点，即数量之和大于双倍的最小节点数量大小，则只需重新分配即可。否则需要进行合并操作。

AdjustRoot函数

/**
 * @brief 用于当根结点被删除了一个键值对之后的处理
 *
 * @param old_root_node 原根节点
 * @return bool 根结点是否需要被删除
 * @note size of root page can be less than min size and this method is only called within coalesceOrRedistribute()
 */
bool IxIndexHandle::AdjustRoot(IxNodeHandle *old_root_node) {
    // Todo:
    // 1. 如果old_root_node是内部结点，并且大小为1，则直接把它的孩子更新成新的根结点
    // 2. 如果old_root_node是叶结点，且大小为0，则直接更新root page
    // 3. 除了上述两种情况，不需要进行操作
    if(old_root_node->IsLeafPage() == 0 && old_root_node->GetSize() == 1){
        IxNodeHandle *new_root = FetchNode(old_root_node->ValueAt(0));
        new_root->SetParentPageNo(INVALID_PAGE_ID);
        file_hdr_.root_page = new_root->GetPageNo();
        release_node_handle(*old_root_node);
        buffer_pool_manager_->UnpinPage(new_root->GetPageId(), true);
        return true;
    }
    else if(old_root_node->IsLeafPage() == 1 && old_root_node->GetSize() == 0){
        file_hdr_.root_page = INVALID_PAGE_ID;
        release_node_handle(*old_root_node);
        return true;
    }
    return false;
}

如果旧根节点是内部节点，并且删除后大小为1，由于其还有孩子节点，孩子节点接替旧根节点成为新的根节点。如果旧根节点是叶节点，并且删除后大小为0，那么整根树都为空，直接将root_page置空即可。

Redistribute函数

/**
 * @brief 重新分配node和兄弟结点neighbor_node的键值对
 * Redistribute key & value pairs from one page to its sibling page. If index == 0, move sibling page's first key
 * & value pair into end of input "node", otherwise move sibling page's last key & value pair into head of input "node".
 *
 * @param neighbor_node sibling page of input "node"
 * @param node input from method coalesceOrRedistribute()
 * @param parent the parent of "node" and "neighbor_node"
 * @param index node在parent中的rid_idx
 * @note node是之前刚被删除过一个key的结点
 * index=0，则neighbor是node后继结点，表示：node(left)      neighbor(right)
 * index>0，则neighbor是node前驱结点，表示：neighbor(left)  node(right)
 * 注意更新parent结点的相关kv对
 */
void IxIndexHandle::Redistribute(IxNodeHandle *neighbor_node, IxNodeHandle *node, IxNodeHandle *parent, int index) {
    // Todo:
    // 1. 通过index判断neighbor_node是否为node的前驱结点
    // 2. 从neighbor_node中移动一个键值对到node结点中
    // 3. 更新父节点中的相关信息，并且修改移动键值对对应孩字结点的父结点信息（maintain_child函数）
    // 注意：neighbor_node的位置不同，需要移动的键值对不同，需要分类讨论
    if(index == 0){
        node->insert_pair(node->page_hdr->num_key, neighbor_node->get_key(0), *neighbor_node->get_rid(0));
        neighbor_node->erase_pair(0);
        maintain_child(node, node->page_hdr->num_key - 1);
        maintain_parent(neighbor_node);
    }
    else{
        int neighbor_pos = neighbor_node->page_hdr->num_key -1;
        node->insert_pair(0, neighbor_node->get_key(neighbor_pos), *neighbor_node->get_rid(neighbor_pos));
        neighbor_node->erase_pair(neighbor_pos);
        maintain_child(node, 0);
        maintain_parent(node);
    }
}

根据兄弟节点为前驱后驱分成两种情况讨论。由于是node节点被删除，所以需要neighbor_node让出多余的键值对给node节点。需要注意第page_hdr->num_key个键值对位于page_hdr->num_key - 1处。

如果兄弟节点是前驱节点，那么neighbor_node让出最后一个键值对给node，放在node的最前面。由于node节点第一个键值对发生变化，则需要使用maintain_parent函数。

如果兄弟节点是后驱节点，那么neighbor_node让出第一个键值对给node，放在node的最后。由于neighbor_node节点第一个键值对发生变化，则需要使用maintain_parent函数。

Coalesce函数

/**
 * @brief 合并(Coalesce)函数是将node和其直接前驱进行合并，也就是和它左边的neighbor_node进行合并；
 * 假设node一定在右边。如果上层传入的index=0，说明node在左边，那么交换node和neighbor_node，保证node在右边；合并到左结点，实际上就是删除了右结点；
 * Move all the key & value pairs from one page to its sibling page, and notify buffer pool manager to delete this page.
 * Parent page must be adjusted to take info of deletion into account. Remember to deal with coalesce or redistribute
 * recursively if necessary.
 *
 * @param neighbor_node sibling page of input "node" (neighbor_node是node的前结点)
 * @param node input from method coalesceOrRedistribute() (node结点是需要被删除的)
 * @param parent parent page of input "node"
 * @param index node在parent中的rid_idx
 * @return true means parent node should be deleted, false means no deletion happend
 * @note Assume that *neighbor_node is the left sibling of *node (neighbor -> node)
 */
bool IxIndexHandle::Coalesce(IxNodeHandle **neighbor_node, IxNodeHandle **node, IxNodeHandle **parent, int index,
                             Transaction *transaction) {
    // Todo:
    // 1. 用index判断neighbor_node是否为node的前驱结点，若不是则交换两个结点，让neighbor_node作为左结点，node作为右结点
    // 2. 把node结点的键值对移动到neighbor_node中，并更新node结点孩子结点的父节点信息（调用maintain_child函数）
    // 3. 释放和删除node结点，并删除parent中node结点的信息，返回parent是否需要被删除
    // 提示：如果是叶子结点且为最右叶子结点，需要更新file_hdr_.last_leaf
    if(index == 0){
		std::swap(*neighbor_node, *node);
		index++;
	}
	int before_num = (*neighbor_node)->GetSize();
    (*neighbor_node)->insert_pairs(before_num, (*node)->get_key(0), (*node)->get_rid(0), (*node)->GetSize());
    int after_num = (*neighbor_node)->GetSize();
    for(int i = before_num; i < after_num; ++i)
        maintain_child(*neighbor_node, i); 
    if((*node)->GetPageNo() == file_hdr_.last_leaf){
        file_hdr_.last_leaf = (*neighbor_node)->GetPageNo();
    }
    erase_leaf(*node);
    release_node_handle(**node);
    (*parent)->erase_pair(index);
    return CoalesceOrRedistribute(*parent, transaction);
}

任务2.4 B+树索引并发控制

任务要求

本任务要求修改IxIndexHandle类的原实现逻辑，让其支持对B+树索引的并发查找、插入、删除操作。

数据库任务二 索引管理

任务2.1 B+树的查找 && 任务2.2 B+树的插入

任务要求

（1）结点内的查找

（2）B+树的查找

（3）结点内的插入

（4）B+树的插入

通关截图

代码分析

（1）结点内的查找

lower_bound函数

upper_bound函数

LeafLookup函数

InternalLookup函数

（2）B+树的查找

FindLeafPage函数

GetValue函数

（3）结点内的插入

insert_pairs函数

insert函数

（4）B+树的插入

insert_entry函数

split函数

InsertIntoParent函数

任务2.3 B+树的删除

任务要求

（1）结点内的删除

（2）B+树的删除

通关截图

代码分析

（1）结点内的删除

erase_pair函数

remove函数

（2）B+树的删除

delete_entry函数

CoalesceOrRedistribute函数

AdjustRoot函数

Redistribute函数

Coalesce函数

任务2.4 B+树索引并发控制

任务要求

通关截图

数据库任务二索引管理