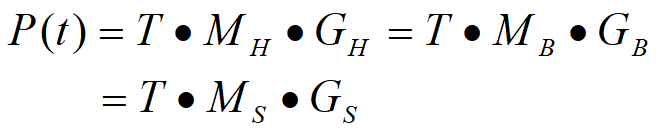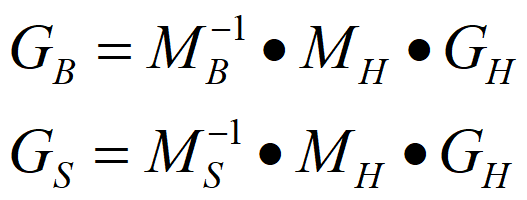计算机图形学概述

计算机图形学（Computer Graphics,CG）是研究怎样用数字计算机生成、处理和显示图形的一门学科

图形：计算机图形学的研究对象

构成图形的要素

  • 几何要素：刻画形状的点、线、面、体等几何要素

  • 非几何要素：反映物体表面属性或材质的灰度颜色等非几何要素。

图形主要分为两类：

  • 基于线条信息表示的，如工程图、等高线地图、曲面的线框图等

  • 明暗图(Shading)，也就是通常所说的真实感图形。

表示图形的方法

  • 点阵法：枚举出图形中所有的点来表示图形，强调图形由点构成，及其点的属性（颜色），这类图形称为像素图或图像。

  • 参数法：由图形的形状参数和属性参数来表示图形，这类图形称为参数图或简称图形。

    • 形状参数：方程或分析表达式的系数，线段的端点坐标等。
    • 属性参数：颜色、线型等。

图像纯指计算机内以位图(Bitmap)形式存在的灰度信息

图形含有几何属性，或者说更强调场景的几何表示，是由场景的几何模型和景物的物理属性共同组成的

image-20230111160901801

计算机图形学的应用

  • 图形用户界面(GUI)
  • 计算机辅助设计与制造（CAD/CAM）
  • 科学计算可视化(Scientific Visualization)
  • 文化和艺术
  • 数字娱乐
  • 数字娱乐

二维图形的级别光栅图形学算法

图形显示设备

CRT显示器指基于阴极射线管（CRT Cathode－Ray Tube）的监视器。

组成：包括电子枪、聚焦系统、加速结构、偏转系统、荧光屏

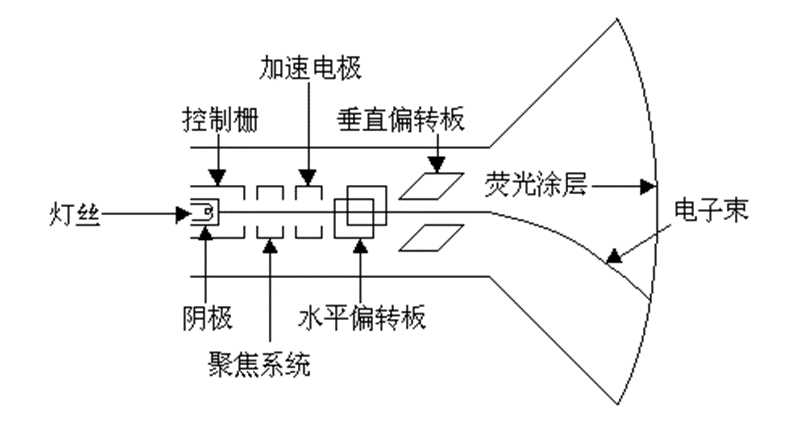
image-20230111171414480
  • 电灯丝，阴极和控制栅组成。阴极由灯丝加热发出电子束。控制栅通过调节负电压高低来控制电子数量，即控制荧光屏上相应点的亮度。
  • 聚焦系统：保证电子束在轰击屏幕时，汇聚成很细的点。
  • 加速电极：加正的高压电（几万伏），使电子束高速运动。
  • 偏转系统：控制电子束，静电场或磁场，产生偏转。电子束要到达屏幕的边缘时，偏转角度就会增大。到达屏幕最边缘的偏转角度被称为最大偏转角。最大偏转角是衡量系统性能的最重要的指标，显示器长短与此有关。CRT显示器屏幕越大整个显象管就越长。
  • 刷新频率：要保持荧光屏上有稳定的图象就必须不断地发射电子束。刷新一次指电子束从上到下将荧光屏扫描一次。只有刷新频率高到一定值后，图象才能稳定显示。60Hz人眼才能感觉到屏幕不闪烁，一般必须有85Hz以上的刷新频率才能使人眼觉得舒服。

CRT固有的物理结构限制了它向更广的显示领域发展。

  • 屏幕的加大必然导致显象管的加长，显示器的体积必然要加大，在使用时候就会受到空间的限制。
  • CRT显示器是利用电子枪发射电子束来产生图像，容易受电磁波干扰。
  • 长期电磁辐射会对人们健康产生不良影响。

LCD（Liquid Crystal Display液晶显示器）是由六层薄板组成的平板式显示器。

液晶是一种介于液体和固体之间的特殊物质，它具有液体的流态性质和固体的光学性质。当液晶受到电压的影响时，就会改变它的物理性质而发生形变，此时通过它的光的折射角度就会发生变化，而产生色彩。

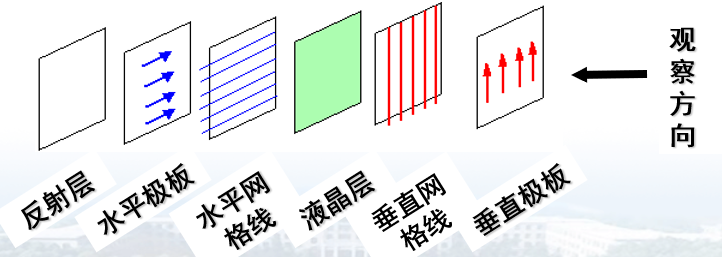
image-20230111173559899

LCD基本技术指标

  • 可视角度：视线与屏幕中心法向成一定角度时，人们就不能清晰地看到屏幕图象，而那个能看到清晰图象的最大角度被我们称为可视角度。一般所说的可视角度是指左右两边的最大角度相加。工业上有CR10（Contrast Ratio）、CR5两种标准来判断液晶显示器的可视角度。
  • 点距与分辨率：液晶屏幕的点距就是两个液晶颗粒（光点）之间的距离，一般0.28~0.32mm就能得到较好的显示效果。分辨率是指液晶显示器含有的液晶颗粒，比如1024×768的含义就是指该液晶显示器含有1024×768个液晶颗粒。

LCD显示器优点

  • 外观小巧精致，厚度只有6.5~8cm左右 。
  • 由于液晶象素总是发光，只有加上不发光的电压时该点才变黑，所以不会产生CRT那样的因为刷新频率低而出现的闪烁现象。
  • 工作电压低，功耗小，节约能源。
  • 没有电磁辐射，对人体健康没有任何影响

图元的扫描转换

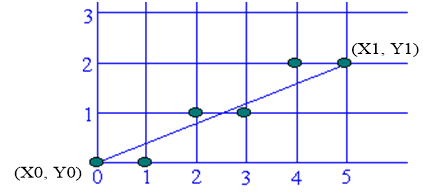
image-20230118115204834

定义：直线的扫描转换是指在二维栅格上计算位于该直线上或充分靠近它的一串象素坐标(光栅化)，并以此像素集近似替代原连续直线段在屏幕上显示的过程。直线由两个端点坐标确定。

要求

  • 观感好，象素分布均匀
  • 误差小，象素尽可能接近数学理想坐标
  • 速度快，避免乘除法和浮点数运算

基本增量算法DDA

最简单、最容易想到的策略，这种方法直观，但效率太低 ，因为每一步需要用浮点计算一次乘法、一次加法和一次取整运算。增量算法在此基础上进行改进。

已知过端点P0 (x0, y0)，P1(x1, y1)的直线段L：$y=kx+B$

  • 计算直线斜率$k=\Delta y/\Delta x=(y_1-y_0)/(x_i-x_0)$
  • 从直线最左端点开始，x每次递增1个单位，对x计算$y_i=kx_i+B$
  • 显示坐标为$(x_i,floor(0.5+y_i))$的象素。

增量算法：在一个迭代算法中，如果每一步的值是用前一步的值加上一个增量来获得，则称为增量算法。增量算法可以避免乘法运算。

推导公式：$y_{i+1}=kx_{i+1}+B=k(x_i+\Delta x)+B=y_i+k\Delta x=y_i+k$

算法描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void DDA (int x0, int y0, int x1, int y1， int Color)
{
	int x;
	double dx,dy,y,k;
	dx = x1-x0;
	dy = y1-y0;
	k = dy/dx;   
	y = y0;
   	for(x = x0; x < = x1; x++)
   	{
       	WritePixel(x, (int)(y + 0.5), Color);
       	y += k;
   	}  
}

需要注意的是上述算法仅适用于$|k|<= 1$的情况，否则会存在丢失像素坐标的情况。

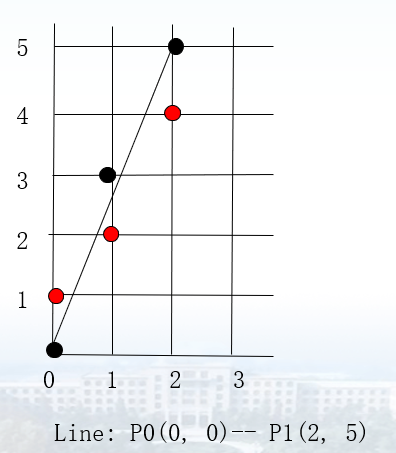
image-20230118172312306
习题：写出DDA算法，使之能扫描转换各种斜率的直线段，包括垂直和水平的线段。

中点线算法（Midpoint）

在DDA算法中，需要采用浮点加法，且每一步都必须对y进行舍入取整，不利于硬件实现。

假定直线斜率0<k<1，且已确定点亮象素点$P(xp,yp)$,则下一个与直线最接近的像素可能是其右边的第一个像素E(称为东像素)，也可能是其右上方的第一个像素NE(称为东北像素) 。假设Q是直线与栅格线$x=x_p+1$的交点，M为E和NE的中点。

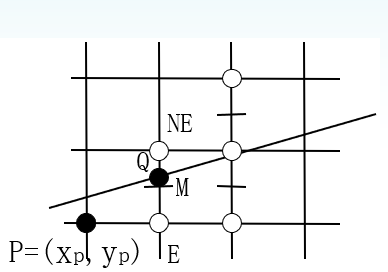
image-20230118191519385

假设直线方程为：$F(x,y)=ax+by+c=0$，则$a=y_0-y_1$，$ b=x_1-x_0$，$c=x_0y_1-x_1y_0$

当点在直线上时$F(x)=0$，点在直线上方时$F(x)>0$，点在直线下方时$F(x)<0$

构造判别式$d=F(M)=F(x_p+1,y_p+0.5)=a(x_p+1)+b(y_p+0.5)+c$

  • 若$d<0$，当M在Q的下方，NE离直线更近，取NE， 那么下一个像素的中点判别式为

$d_1=F(x_p+2,y_p+1.5)=a(x_p+2)+b(y_p+1.5)+c=d+a+b$

  • 若$d>=0$，当M在Q的上方，E离直线更近，取E，那么下一个像素的中点判别式为

$d_1=F(x_p+2,y_p+0.5)=a(x_p+2)+b(y_p+0.5)+c=d+a$

画线从$(x_0,y_0)$开始，d的初值$d_0=F(x_0+1, y_0+0.5)=a(x_0+1)+b(y_0 +0.5)+c=F(x_0,y_0)+a+0.5b=a+0.5b$

由于只用d的符号作判断，为了只包含整数运算，可以用2d代替d来摆脱小数，提高效率。同理，d1和d2的值也都被乘以2。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void MidpointLine (int x0,int y0,int x1, int y1,int color){
    int a = y0 - y1;
    int b = x1 - x0;
    int d = 2 * a + b;
    int d1 = 2 * a;
    int d2 = 2 * (a + b);
    int x = x0;
    int y = y0;
    WritePixel(x, y, color);
    while(x <= x1){
        if(d < 0){
            x++;
            y++;
            d += d2;
        }
     	else{
        	x++; 
            d += d1;
     	}
     	WritePixel (x, y, color);
     }
}
习题：利用中点线算法，使之能扫描转换斜率-1<k<0的直线段。

圆的扫描转换

假设圆的方程为$X^2+Y^2=R^2$，那么可知Y点坐标$Y=\sqrt{R^2 - X^2}$

当X取整数时，Y也须取整。

缺点：浮点运算，开方，取整，不均匀。

假设圆的方程为$x=Rcos\theta$，$y=Rsin\theta$

画点$(Rcos\theta，Rsin\theta)$，$\theta$从0到90，再对称，可避免点分布不均。

缺点：采用浮点运算、乘法运算、取整运算，效率不高。

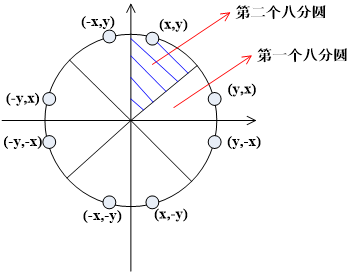
image-20230119121904021 
1
2
3
4
5
6
7
8
9
10
11
void CirclePoints (float x,float y,int color)
     {
	WritePixel (x, y, color);
	WritePixel (y, x, color);
	WritePixel (y, -x, color);
	WritePixel (x, -y, color);
	WritePixel (-x, -y, color);
	WritePixel (-y, -x, color);
	WritePixel (-y, x, color);
	WritePixel (-x, y, color);
}

利用圆的对称性，只须讨论1/8圆。此处只考虑第二个8分圆。

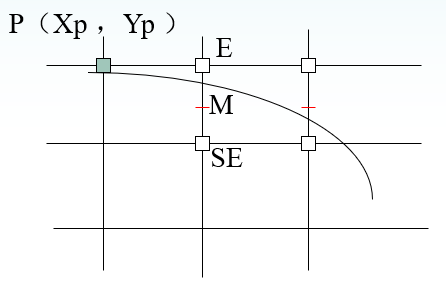
image-20230119122442341

P为当前点亮象素，那么，下一个点亮的象素可能是$E(X_p+1, Y_p)$或$SE(X_p+1, Y_p-1)$。

构造函数：$F(X, Y)=X^2+Y^2-R^2$ ；则

设M为E、SE间的中点，则$M=(X_p+1, Y_p-0.5)$

  • $F(X, Y)=0$，（X，Y）在圆上，取SE
  • $F(X, Y)<0$，（X，Y）在圆内，取E
  • $F(X, Y)>0$，（X，Y）在圆外，取SE

若d<0，则E为下一个象素，那么再下一个象素的判别式为，说明d的增量为$2x_p+3$

$d1=F(x_p+2, y_p-0.5)=(x_p+2)^2+(y_p-0.5)^2-R^2=d+2x_p+3$

若d>=0，则SE为下一个象素，那么再下一个象素的判别式为，说明d的增量为$2(x_p-y_p)+5$

$d2=F(x_p+2, y_p-1.5)=(x_p+2)^2+(y_p-1.5)^2-R^2=d+2x_p+3-2y_p+2=2(x_p-y_p)+5$

画圆从(0, R)开始，d的初值$d0=F(1, R-0.5)=1+(R-0.5)^2-R^2=1.25-R$

image-20230119132306042

由于只用d 的符号作判断，为了只包含整数运算，可以用4d代替d来摆脱小数，提高效率。同理，d1和d2的值也都被乘以4。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
MidpointCircle2(int r, int color){
    int x=0; 
    int y=r; 
	int d=5-4*r;
    WritePixel(x,y,color);
    while(x<y){
        if(d<0){
            d+=8*x+12;
            x++; 
        }
        else{
            d+=8*(x-y)+20;
            x++;
            y--;
        }
		WritePixel(x,y,color);
    }
}

使用e=d-0.25代替d，e0=1-R

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
MidpointCircle3(int r, int color){
    int x=0;
    int y=r; 
	int d=1-r;
    WritePixel(x,y,color);
    while(x<y){
        if(d<0){
            d+=2*x+3;
            x++
        }
        else{
            d+=2*(x-y)+5;
            x++;
            y--;
        }
		WritePixel(x,y,color);
    }
}

习题：请利用中点圆算法实现第一个八分圆的扫描转换。

矩形、多边形填充

共享边界如何处理？
原则：左闭右开，下闭上开，对单个多边形区域，它损失了中心落在右、上边界的像素。

顶点表示：用多边形顶点的序列来刻划多边形。直观、几何意义强、占内存少；不能直接用于显示。

点阵表示：用位于多边形内的象素的集合来刻划多边形。失去了许多重要的几何信息；但它是光栅显示系统显示时所需的表示形式，易于面着色。

逐点判断法

算法原理：逐个判断绘图窗口内的像素，确定是否在多边形区域内，从而求出位于多边形区域内的像素集合。

1
2
3
4
5
6
7
8
9
void FillPolygonPbyP(Polygon *P,int color){
    int x,y;	
    for(y = ymin;y <= ymax;y++){
        for(x = xmin;x <= xmax;x++){
            if(IsInside(P,x,y))
                WritePixel(x,y, color);
        }
    }
}
如何判断点在多边形的内外关系？

射线法：

  1. 从待判别点v发出射线
  2. 求交点个数k
  3. k的奇偶性决定了点与多边形的内外关系

累计角度法：

  1. 从v点向多边形P顶点发出射线，形成有向角$\theta_i$
  2. 计算有相角的和，得出结论
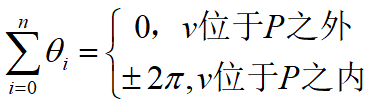
image-20230121180810495

逐点判断的算法虽然程序简单，但不可取。原因是速度太慢，主要是由于该算法割断了各象素之间的联系，孤立地考察各象素与多边形的内外关系，使得几十万甚至几百万个象素都要一一判别，每次判别又要多次求交点，需要做大量的乘除运算，花费很多时间。

扫描线算法

目标：利用相邻像素之间的连贯性，提高算法效率

处理对象：非自交多边形（边与边之间除了顶点外无其它交点）

算法原理：将多边形填充分解为一条条的扫描线填充，对任一条扫描线，确定该扫描线与多边形边的交点位置，自左向右存储，并对每对内部交点间的像素进行填充。

规则1：X为小数，即交点落于扫描线上两个相邻像素之间

  • 交点位于左边之上，向右取整
  • 交点位于右边之上，向左取整

规则2：边界上象素的取舍问题，避免填充扩大化。

边界象素：规定落在右上边界的象素不予填充。具体实现时，只要对扫描线与多边形的相交区间左闭右开

规则3：扫描线与多边形的顶点相交时，交点的取舍，保证交点正确配对。

计算交点个数时，仅对边的ymin顶点计数，ymax顶点不计数。依然遵循下闭上开的原则。

步骤：
  1. 求交：求扫描线与多边形各边交点
  2. 排序：按 x 递增顺序对交点排序
  3. 交点匹配：1－2，3－4，5－6等
  4. 填充：填充每对交点间在多边形区域内部的象素。

假定已经求解出扫描线y=e和多边形边的所有交点，需递推出扫描线y=d=e+1与多边形各边的交点，求解可分为两类：

  • 边既和y=e相交，又和y=d相交。若x为其中某条边与y=e的交点横坐标，k为该边的斜率，则此边与y=d的交点横坐标x’=x+1/k；
  • 边只与y=d相交，不与y=e相交，即新出现的边。此时，这些边的下端点就是交点，不用计算。
特殊情况处理

水平边在算法中不起作用，预处理阶段将其去掉。

尖角填充区域狭窄，许多扫描线上按规则一个象素都不能画。进行反走样处理。

数据结构与算法

扫描线算法中采用了较灵活的数据结构，即边的分类表ET(Edge Table)和活动边表AET(Active Edge Table)，两个表结构中的基本元素都是边结构。边结构定义为：

1
2
3
4
5
6
typedef struct  　{
   　int ymax; // 边的上端点的y值
  　 float x;　// ET表中为边的下端点的x值；AET中为当前扫描线与边的交点的x值
   　float dx; // 单位高度x方向偏移量（即边的斜率的倒数）
   　E *nextEdge ;  // 指向下一条边的指针
}E;

边表ET：边表ET是按边的下端点的y坐标对非水平边进行分类的,下端点y坐标值等于i的边属于第i类，绘图窗口中有多少条扫描线，ET就分为多少类，同一类中的边按其下端点的x值(x值相等的，按$\Delta$x值)增序排列。

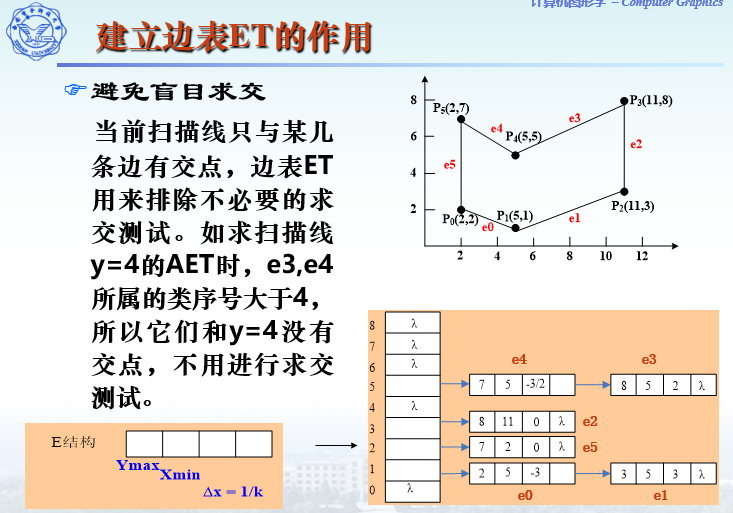
image-20230121191333993

活动边表AET：活动边表AET由与当前扫描线相交的边组成，它记录多边形的边和当前扫描线的所有交点的x坐标，并且随着扫描线的递增而不断变化。

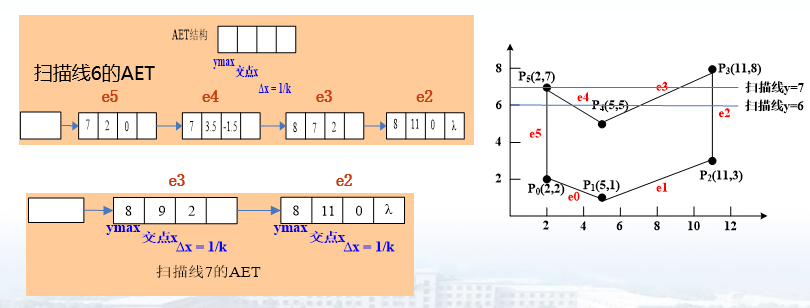
image-20230121191752500

image-20230121191215894

习题：已知下图多边形顶点坐标顺序为（1，1）（2，4）（4，1）（4，6）（0，6）。用扫描线算法对其实现填充时，边表ET和全部活动边表AET的内容。

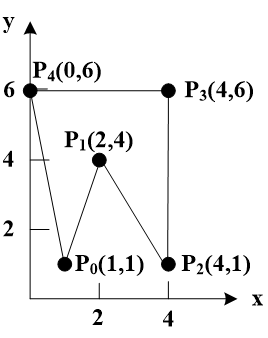
image-20230121192107598

增量算法，通过上一条扫描线得到的x交点坐标，计算下一点的x坐标，即$x_{i+1}=x_i+(y_{i+1}-y_i)*\frac{1}{k}=x_i+\Delta x$

当边在ET表中出现时将其添加进AET表，当扫描线等于边的$y_{max}$时，将边从AET表中删除

直线段剪裁

直接求交算法

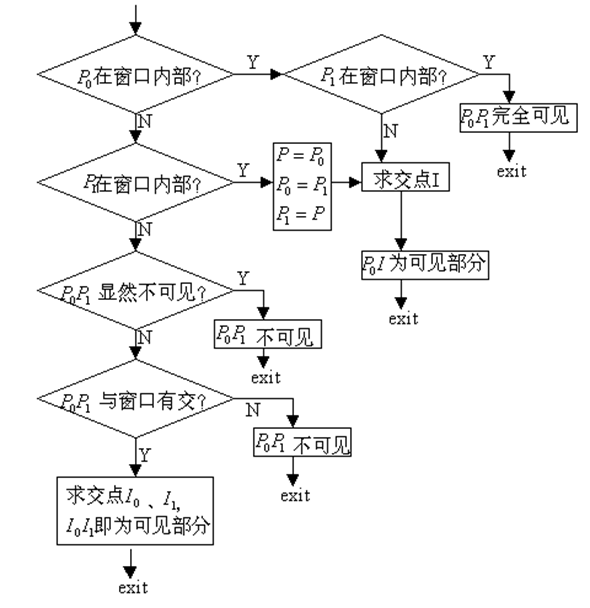
image-20230123114146080 image-20230123114333274

Cohen-Sutherland裁剪

基本思想：对于每条线段P1P2分为三种情况处理

  • 若P1P2完全在窗口内，则显示该线段P1P2。
  • 若P1P2明显在窗口外，则丢弃该线段。
  • 若线段不满足（1）或（2）的条件，则在交点处把线段分为两段。其中一段完全在窗口外，可弃之。然后对另一段重复上述处理。

编码：平面被分为9个区域，每个区域内统一编码。任一个点P(x,y)用四位01编码$C_tC_bC_rC_l$表示。

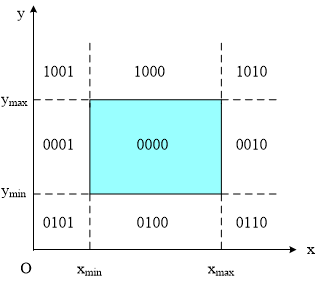
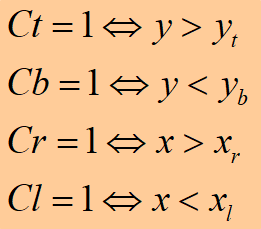
image-20230123114714120 image-20230123114818337
  • 若P1P2完全在窗口内code1=0,且code2=0,则完全显示；
  • 若P1P2明显在窗口外code1&code2≠0，则线段舍弃；
  • 在交点处把线段分为两段。其中一段完全在窗口外，可弃之。然后对另一段重复上述处理。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
//该数据结构记录端点编码，
//all元素表示端点编码.
typedef struct{
	unsigned all;
	unsigned top,bottom, right,left;
}Code;
//矩形数据结构，表示裁剪窗口
typedef struct{
	int xmin,xmax,ymin,ymax;
}Rectangle;
//计算点(x,y)的编码
void CompCode(float x,float y,Rectangle *rect,Code *code){
	code->all = 0; //该值即为端点的4位编码CtCbCrCl
	code->top = code->bottom = 0;
	if(y>(float)rect->ymax){
		code->top = 1;
		code->all += 8;
	}
	else if(y<(float)rect->ymin){
		code->bottom = 1;
		code->all += 4;
	}
	code->right = code->left = 0;
	if(x>(float)rect->xmax){
		code->right = 1;
		code->all += 2;
	}
	else if(x<(float)rect->xmin){
		code->left = 1;
		code->all += 1;
	}	
}    
//Cohen-Sutherland裁剪函数
void CohenSutherlandLineClip(float x0,float y0,float x1,float y1,Rectangle *rect){
	bool accept,done;   //接受线段、拒绝线段
	Code code0,code1; //两个端点的编码
	Code *outCode;    //指向窗口外的端点
	float x,y;                //线段与窗口边的交点坐标
	accept = FALSE;
	done = FALSE;
	//计算两端点编码
	CompCode(x0,y0,rect,&code0);
	CompCode(x1,y1,rect,&code1);
	while(!done){
		if(code0.all==0 && code1.all==0){ //完全可见，接受线段
			accept = TRUE;
			break;
		}
		else if(code0.all & code1.all!=0){   //显然不可见，拒绝线段
			done = TRUE;
			break;
		}
		else{    //需要求交测试
			if(code0.all!=0)   //判断哪一点位于窗口之外
				outCode = &code0;
			else
				outCode = &code1;    
			if(outCode->top){     //线段与窗口的上边求交
				x = x0+(x1-x0)*(rect->ymax-y0)/(y1-y0);
				y = (float)rect->ymax;
			}
			else if(outCode->bottom){   //线段与窗口的下边求交
				x = x0+(x1-x0)*(rect->ymin-y0)/(y1-y0);
				y = (float)rect->ymin;
			}
			else if(outCode->right){   //线段与窗口右边求交
				x = (float)rect->xmax;
				y = y0+(y1-y0)*(rect->xmax-x0)/(x1-x0);
			}
			else if(outCode->left){    //线段与窗口左边求交
				x = (float)rect->xmin;
				y = y0+(y1-y0)*(rect->xmin-x0)/(x1-x0);
			}
			//舍弃外端点和交点间的线段，将交点作为新端点继续循环
			if(outCode->all == code0.all){    //交点作为新的p0点
				x0 = x;
				y0 = y;
				CompCode(x0,y0,rect,&code0);
			}
			else{    //交点作为新的p1点
				x1 = x;
				y1 = y;
				CompCode(x1,y1,rect,&code1);
			}
		}
	}
	if(accept){  //显示线段的可见部分
		Line((int)x0,(int)y0,(int)x1,(int)y1);
	}
}

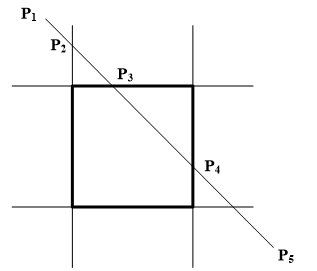
习题：CohenSutherland矩形裁剪直线段算法中，平面被划分成9个区域，可按照左上右下的顺序对各区域进行4位编码。
（1）请画图并在对应的子区域中标出该区域的编码值；
（2）对下图中所示的线段进行裁剪，假设求交时窗口的选择顺序为左边、上边、右边、下边，请给出裁剪步骤，并列出各端点编码。

image-20230123120504656

多边形剪裁

Sutherland-Hodgman算法（逐边裁剪算法）

分割处理策略：将多边形关于矩形窗口的裁剪分解为多边形关于窗口四边所在直线的裁剪。

流水线过程(左上右下)：前边的结果是后边的输入。

基本思想是一次用窗口的一条边裁剪多边形。

考虑窗口的一条边以及延长线构成的裁剪线，该线把平面分成两个部分:内部；外部

多边形的各条边的两端点S、P。它们与裁剪线的位置关系只有四种

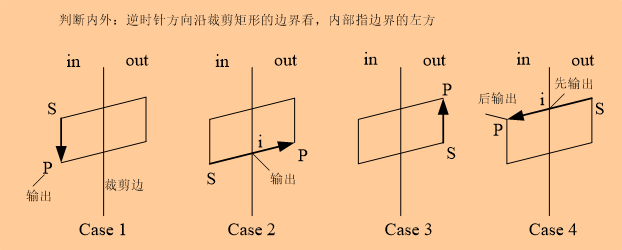
image-20230123165550060

针对每一条裁剪边，沿多边形的边从顶点vn移动到v0,再顺序移动回vn,每次移动，检测连续的两个顶点与裁剪边的相互关系。每步移动，对于裁剪后的多边形顶点序列，可能会增加0个、1个或2两个顶点。假定在上一次循环操作中已经处理了起始点S,则输出分四种情况：

  1. 输出顶点P；
  2. 输出线段SP与裁剪线的交点i；
  3. 输出0个顶点；
  4. 输出线段SP与裁剪线的交点i和终点P。

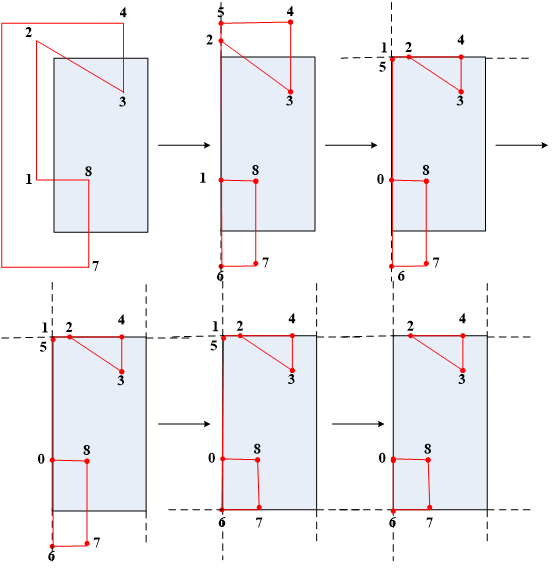
image-20230123165758684

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#define MAX 100
//点结构
typedef struct{
	float x,y;
}vertex;
vertex clipBoundary[2];         //表示裁剪边顶点
vertex inVertexArray[MAX];//表示源多边形顶点序列
vertex outVertexArray[MAX];//表示输出裁剪多边形的顶点序列

//判断顶点是否在裁剪边内侧，若在，返回TRUE
bool Inside(vertex testVertex, vertex *clipBoundary){
	if(clipBoundary[1].x>clipBoundary[0].x) //下裁剪线
		if(testVertex.y>=clipBoundary[0].y) return TRUE;
	if(clipBoundary[1].x<clipBoundary[0].x) //上裁剪线
		if(testVertex.y<=clipBoundary[0].y) return TRUE;
	if(clipBoundary[1].y>clipBoundary[0].y) //右裁剪线
		if(testVertex.x<=clipBoundary[0].x) return TRUE;
	if(clipBoundary[1].y<clipBoundary[0].y) //左裁剪线
		if(testVertex.x>=clipBoundary[0].x) return TRUE;
	return FALSE;
}  
//添加一个新顶点到输出顶点数组outVertexArray中
void Output(vertex newVertex,int *outLen,vertex *outVertexArray){
	(*outLen) ++;
	outVertexArray[*outLen-1].x = newVertex.x;
	outVertexArray[*outLen-1].y = newVertex.y;
}
//计算多边形的一条边与一条裁剪边的交点
void Intersect(vertex first,vertex second,vertex *clipBoundary,vertex *intersectPt){
	if(clipBoundary[0].y==clipBoundary[1].y){  //水平裁剪边
		intersectPt->y = clipBoundary[0].y;
		intersectPt->x = first.x + (clipBoundary[0].y-first.y)*(second.x-first.x)/(second.y-first.y);
	}
	else{  //垂直裁剪边
		intersectPt->x = clipBoundary[0].x;
		intersectPt->y = first.y +(clipBoundary[0].x-first.x)*(second.y-first.y)/(second.x-first.x);
	}
}
//sutherland-Hodgman多边形裁剪算法
void SutherlandHodgmanPolygonClip(vertex *inVertexArray,vertex *outVertexArray,int inLen, int *outLen,vertex *clipBoundary){
	vertex s,p,i;
	int j;
	*outLen = 0;
	s = inVertexArray[inLen-1]; //从多边形最后一个顶点开始移动
	for(j=0;j<inLen;j++){
		p = inVertexArray[j];
		if(Inside(p,clipBoundary)){ // case1 和 case4
			if(Inside(s,clipBoundary)) //case 1
				Output(p,outLen,outVertexArray);
			else{  //case 4
				Intersect(s,p,clipBoundary,&i);
				Output(i,outLen,outVertexArray);
				Output(p,outLen,outVertexArray);
			}
		}
		else if(Inside(s,clipBoundary)){ //case 2
			Intersect(s,p,clipBoundary,&i);
			Output(i,outLen,outVertexArray);
		}
		s = p;  //顶点继续移动
	}
}

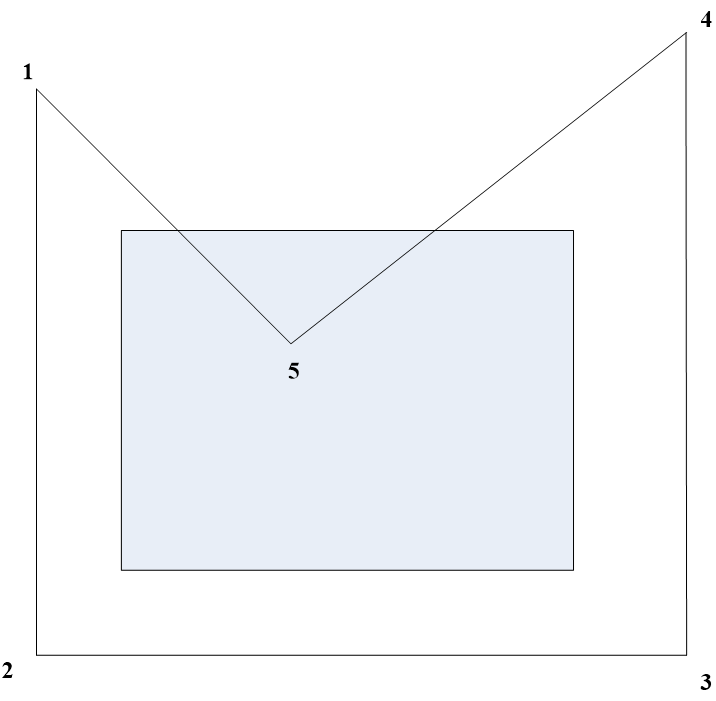
习题：按照左、上、右、下的裁剪顺序模拟Sutherland-Hodgman算法处理。

image-20230123170406785

反走样

用离散量表示连续量引起的失真现象称之为走样(aliasing) 。

光栅图形的走样现象

  • 阶梯状边界；
  • 图形细节失真；
  • 狭小图形遗失：动画序列中时隐时现，产生闪烁。

用于减少或消除走样现象的技术称为反走样(antialiasing)，常用的反走样方法有：

提高分辨率

  • 直线经过两倍的象素，锯齿也增加一倍，

  • 但同时每个阶梯的宽度也减小了一倍，

  • 所以显示出的直线段看起来就平直光滑了一些

方法简单，但代价非常大。显示器的水平、竖直分辩率各提高一倍，则显示器的点距减少一倍，帧缓存容量则增加到原来的4倍，而扫描转换同样大小的图元却要花4倍时间。
而且它也只能减轻而不能消除锯齿问题

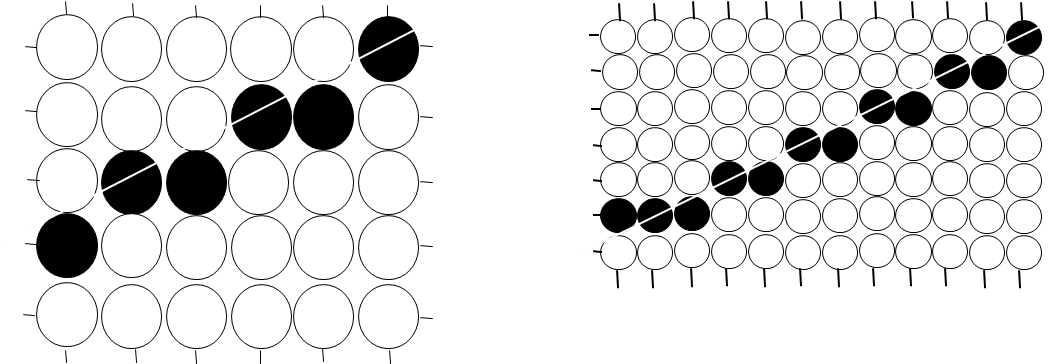
image-20230123170624786

非加权区域采样

两点假设

  1. 象素是数学上抽象的点，它的面积为0，它的亮度由覆盖该点的图形的亮度所决定；
  2. 直线段是数学上抽象直线段，它的宽度为0。

现实

  1. 像素的面积不为0；
  2. 直线段的宽度至少为1个像素；

假设与现实的矛盾是导致走样出现的原因之一

解决方法：改变直线段模型，由此产生算法

方法步骤：

  1. 将直线段看作具有一定宽度的狭长矩形；
  2. 当直线段与某象素有交时，求出两者相交区域的面积；
  3. 根据相交区域的面积，确定该象素的亮度值

加权区域采样

  1. 将屏幕象素分割成n个更小的子象素；
  2. 计算中心点落在直线段内的子象素的个数，记为k，
  3. k/n为线段与象素相交区域面积的近似值

k/n是介于[0,1]之间的实数，用它乘以像素的最大灰度值，即可得到像素实际显示的灰度值。

缺点：象素的亮度与相交区域的面积成正比，而与相交区域落在象素内的位置无关，这仍然会导致锯齿效应。

加权区域采样对非加权区域采样进行了改进，使得相交区域对像素亮度的贡献依赖于该区域与像素中心的距离。对于相同面积的相交区域，当它距离像素中心近时，它对像素亮度的贡献大，反之则小。

图形变换

图形变换是计算机图形学基础内容之一，是图形显示过程中必不可少的一个环节。
几何变换，视窗变换，投影变换

作用：

  • 可由简单图形生成复杂图形；
  • 可由一个图形得到多个图形；
  • 静态图形快速变换，可实现图形的动态显示效果。
  • 把用户坐标系与设备坐标系联系起来；
  • 可用二维图形表示三维形体；

二维基本变换

平移变换

image-20230123182537344

放缩变换

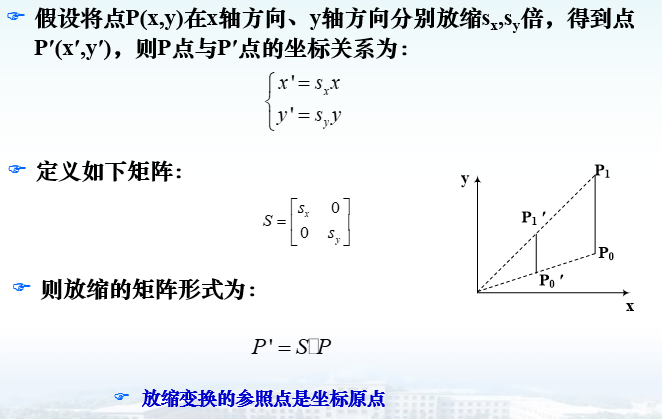image-202301231826006601

旋转变换

image-20230123182629422

对称变换

image-20230123183320807

错切变换

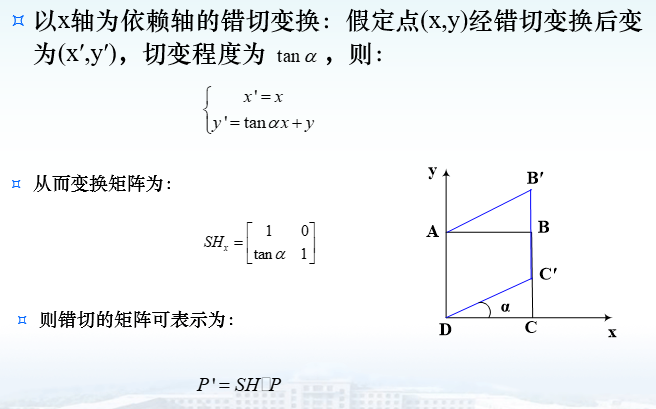
image-20230123183548654 image-20230123183626399

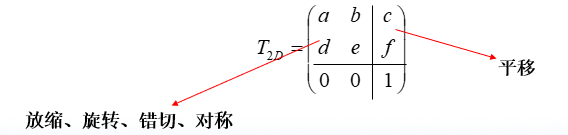
齐次坐标与复合变换

在实际绘图时，常要对图形对象连续做多个变换，如先旋转，再放缩，如果对图形上的每个点依次按照变换矩阵进行计算，计算量较大，如果先将两个变换合成一个复合变换，再进行一次性的矩阵与向量乘法即可。

如果变换中再加入平移变换，变换就不易合成了，因为平移变换为矢量的加法，而其它变换为一个矩阵的乘法，为了使得各种变换的表示形式一致，从而使变换合成更容易，引入了齐次坐标的概念。

所谓齐次坐标表示法就是由n+1维向量表示一个n维向量。如n维向量$(P_1,P_2, … ,P_n)$表示为$(hP_1,hP_2,…,hP_n,h)$，其中h称为哑坐标。

  • h可以取不同的值，所以同一点的齐次坐标不是唯一的。如普通坐标系下的点（2,3）变换为齐次坐标可以是(1,1.5,0.5)(4,6,2)(6,9,3)等等。
  • 普通坐标与齐次坐标的关系为“一对多”
    • 由普通坐标*h→齐次坐标
    • 由齐次坐标÷h→普通坐标
  • 当h=1时产生的齐次坐标称为“规格化齐次坐标”，因为前n个坐标就是普通坐标系下的n维坐标。

由于多对一的映射往往使运算复杂，所以一般齐次坐标指的都是规格化齐次坐标，即(x,y)的齐次坐标为(x,y,1)。

image-20230125212723500
对参考点$F(x_f,y_f)$做旋转变换：

1、把旋转中心F(xf,yf)平移至坐标原点，即X,Y分别平移（-xf,-yf），则

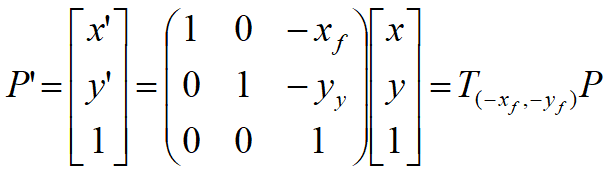
image-20230125214858717

2、进行旋转变换

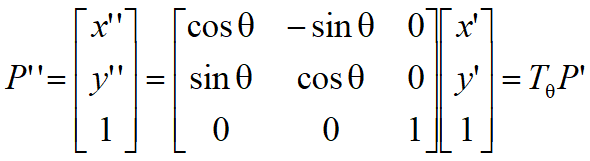
image-20230125214907451

3、将图形平移回原来的位置

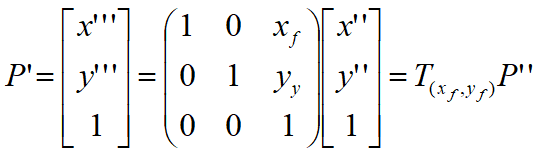
image-20230125214916446

因此变换矩阵：

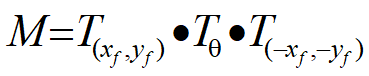
image-20230125214924522
任一图形关于任意轴y=bx+a的对称变换
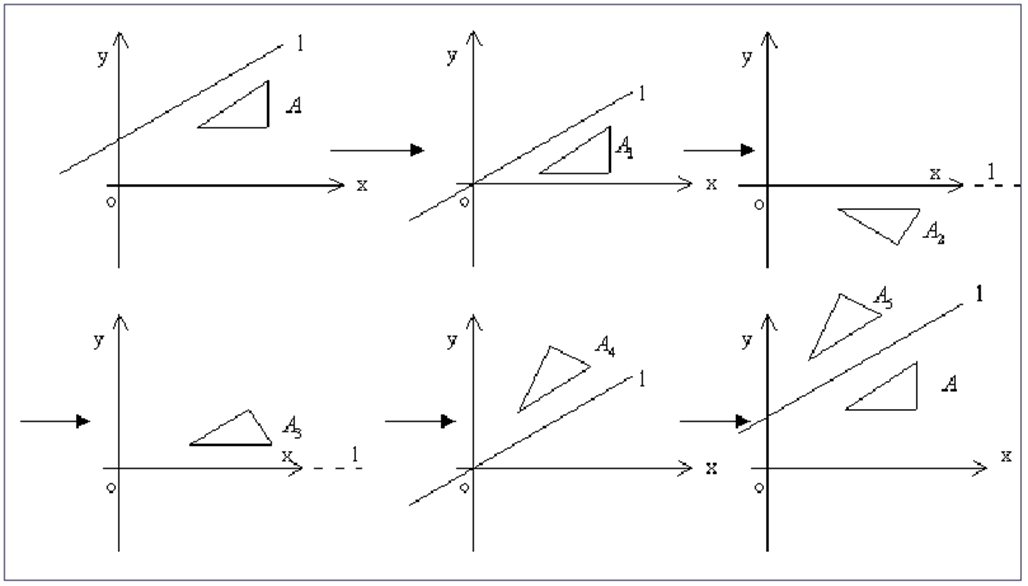
image-20230125223351698

1.将任意轴平移到原点

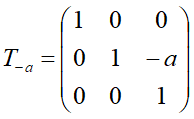
image-20230125223419387

2.将任意轴（已平移后的直线）按顺时针方向旋转θ角，使之与x轴重合

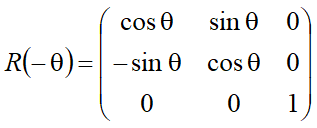
image-20230125223442379

3.图形关于x轴的对称变换

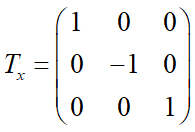
image-20230125223448449

4.将任意轴逆时针旋转θ角

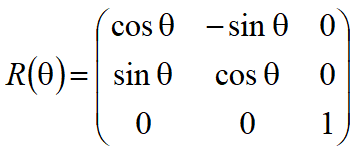
image-20230125223453854

5.将任意轴移回原始位置

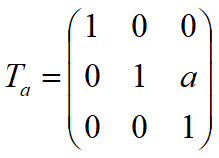
image-20230125225730909

因此

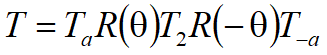
image-20230125225757408

习题：已知三角形ABC各顶点坐标为 A(6,10), B(11,14), C(27,-7) ，试对其进行下列变换，写出变换矩阵，画出变换后的图形。
（1）沿x负向平移10，沿y正平移-15，
（2）再绕原点顺时针旋转90°。

三维几何变换

关于任意参考点的放缩变换

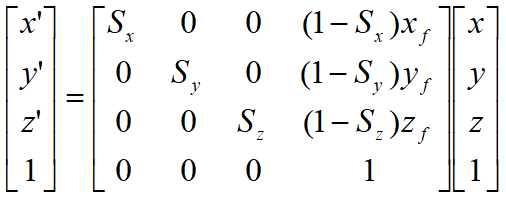
image-20230126000026124

任意参考点平移到坐标原点－>做关于原点的比例变换－>在将参考点移动回原来的位置

绕任意轴的旋转变换
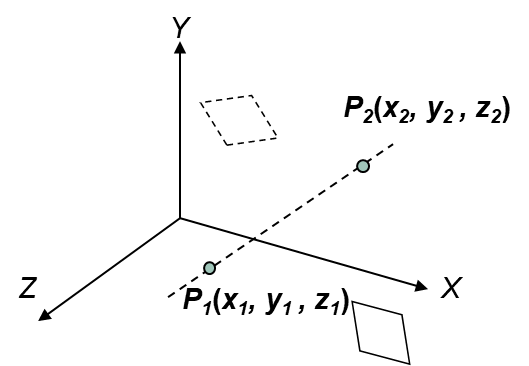
image-20230126010853737

1.将空间直线平移，使P1通过坐标原点: T(-x1, -y1, -z1)

image-20230126010932415

2.绕x轴旋转〆角使之位于XOZ平面内: $R_x(α)$

image-20230126010940617

3.绕y轴顺时针旋转ß角(使之与Z轴重合): $R_y (-\beta)$

image-20230126010946332

4.绕z轴旋转θ角: $R_z(\theta)$

image-20230126011017192

因此，加上逆过程后，绕任意轴旋转的合成变换为：

$M=T(x_1,y_1,z_1)R_x(-\alpha)R_y(\beta)R_z(\theta)R_y(-\beta)Rx(\alpha)T(-x1,-y1,-z1)$

曲线和曲面

参数曲线基础

表示曲线和曲面的基本方法有两大类：非参数表示法（显式表示法、隐式表示法）和参数表示法。

非参数表示法

非参数表示曲线存在的问题：

  • 无法表示斜率为无穷大的情况；

  • 与坐标轴有关；

显式表示法

$y=f(x)$

一个x值与一个y值对应

缺点：不能表示封闭曲线或多值曲线，如不能显式表示圆或椭圆。

隐式表示法

$f(x,y)=0$

给定x，无法准确的给出确切的y。能表示封闭曲线和多值曲线。

优点：易于判断函数f(x，y)是否大于、小于、等于0，即易于判断点和曲线的相对位置关系。（画圆、画直线时都是这样）。

参数表示法

曲线上的任一点的坐标，表示成参数的函数

假定用t表示参数，二维平面曲线上任一点P可表示为$P(t)=[x(t), y(t)]$

空间曲线上任一三维点P可表示为$P(t)=[x(t), y(t), z(t)]$

最简单的参数曲线是直线段，端点为P1、P2的直线段参数方程可表示为$P(t)=P1+(P2-P1)t, t∈[0, 1]$

参数表示法的优越性：

  1. 可以满足形式不变性的要求。

  2. 有更大的自由度来控制曲线、曲面的形状。

    如一条二维三次曲线的显式表示为$y=ax^3+bx^2+cx+d$，只有四个系数控制曲线的形状

    写成参数表示形式为，有8个参数可用

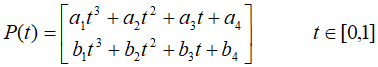
    image-20230127125831087

  3. 对参数表示的曲线、曲面进行几何变换比较方便。

  4. 用切矢量代替了斜率，便于处理斜率为无穷大的情形。 即

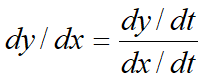
    image-20230127130126284

  5. 规格化的参数变量t∈[0, 1]，使其相应的几何分量是有界的，而不必用另外的参数去定义边界。

三次参数曲线

工程上常用的曲线可以分为两类:

规则曲线

可以用函数或参数方程直接表示的曲线

参数t在一定区间变化，可以求得曲线上不同的坐标点，连接这些坐标点就能在屏幕上画出曲线，t变化间隔越小，曲线画得越精细。

不规则曲线(拟合曲线)

工程中除了用到前述的规则曲线外，还常常遇到这样的情况：已知一些计算值或测试数据，要构造一条光滑曲线，通过或贴近这些离散点数据，这样构造出来的曲线称为拟合曲线。

拟合曲线通常采用二次或三次参数曲线的形式，我们一般采用三次拟合曲线。(原因低于3次，控制曲线形状不够灵活，高于3次，计算量太大，且可能增加不必要的摆动（即振荡））。

主要三类拟合曲线：

  • Hermite曲线
  • Bezier曲线
  • B样条曲线

三次参数曲线的基本特征

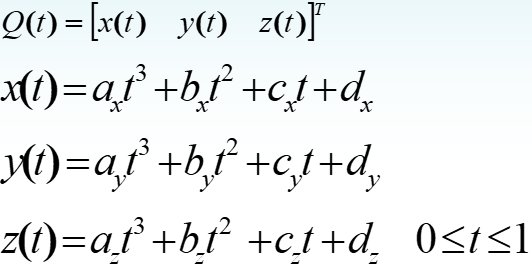
image-20230127131450376

如果曲线用{x=f(t),y=g(t)}的形式来表示:

曲线1为${x=f_1(t),y=g_1(t)}$, 曲线2为${x=f_2(t),y=g_2(t)}$,

几何连续$G^i$ 与参数连续$C^i$

  • G0、C0连续：两条曲线段拼接成一条曲线。
  • G1连续： 两条曲线段拼接点处切向量方向相同。C1则是方向、大小相等
  • Gn连续：两条曲线段拼接点处切向量的n阶导数方向相同。Cn则是n阶导数相等

${f_1(t_1)=f_2(t_2), g_1(t_1)=g_2(t_2)}$这是 C0 G0连续

${f_1’(t_1)=f_2’(t_2), g_1’(t_1)=g_2’(t_2)}$这是 C1连续

$f_1’(t_1)/g_1’(t_1) = f_2’(t_2)/g_2’(t_2)$这是G1连续

${f_1”(t_1)=f_2”(t_2), g_1”(t_1)=g_2”(t_2)}$这是 C2连续

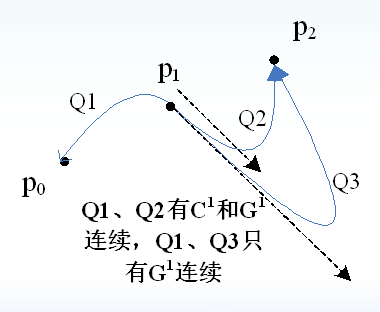
image-20230127135638495 image-20230127183429217

$f_1’’(t_1)=-12t_1+6,g_1’’(t1)=-6,f_2’’(t_2)=12t_2-6,g_2’’(t_2)=27t_2-6$

令$f_1’’(t1)=f_2’’(t2),g_1’’(t_1)=g_2’’(t_2)$得$t_1=1,t_2=0$

所以有$f_1’’(1)=f_2’’(0),g_1’’(1)=g_2’’(0)$，故两条三次曲线达到$C^2$连续

image-20230128171604699

$f_1’(t_1)=2t_1-2,g_1’(t1)=3t^2-4t+1,f_2’(t_2)=2t,g_2’(t_2)=3t^2$

令$f_1’(t1)=f_2’(t2),g_1’(t_1)=g_2’(t_2)$得$t_1=1,t_2=0$

所以有$f_1’(1)=f_2’(0),g_1’(1)=g_2’(0)$，故两条三次曲线达到$C^1$连续

又当$t_1=1,t_2=0$时，$f_1’(t_1)/g_1’(t_1)$或$f_2’(t_2)/g_2’(t_2)$不存在，故两条三次曲线没有$G^1$连续

曲线段可以用端点、切向量和曲线段之间的连续性等约束条件来定义

  • 两个端点和两端点处的切向量定义Hermite曲线；
  • 两个端点和另外两个控制端点切向量的点定义的Bezier曲线；
  • 由四个控制顶点定义的B样条曲线。

$Q(t)=[x(t)\ y(t)\ z(t)]=TC=TM*G$

M为基矩阵

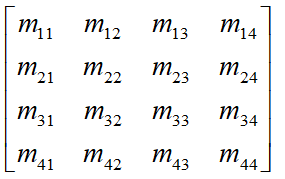
image-20230128175528500

G为四个元素的几何约束行向量矩阵

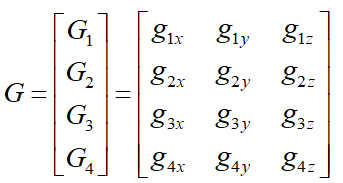
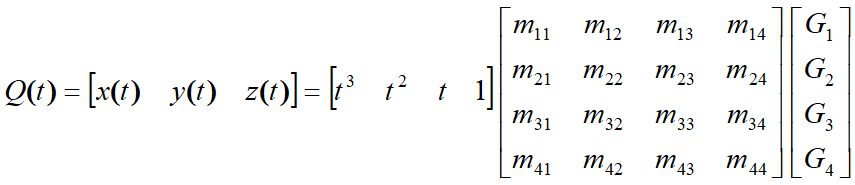
image-20230128175537407 image-20230128175756068

$x(t)=TMG$展开

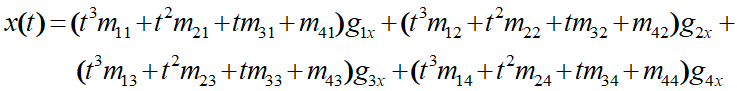
image-20230128175804294

Hermite 曲线

由端点P1、P4和端点处切向量R1、R4的约束确定 ，其几何矩阵为

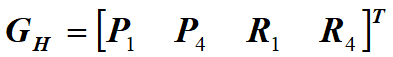
image-20230128172406300

仅讨论其x分量

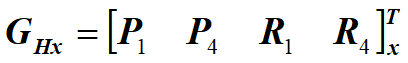
image-20230128172423307

$x(t)=a_xt^3+b_xt^2+c_xt+d_x=TC_x=TM_H*G_{Hx}=[t^3\ t^2\ t\ 1]M_HG_{Hx}$

t=0、1带入，得到其$P_{1x}、P_{4x}$约束

$x(0)=P_{1x}=[0\ 0\ 0\ 1]M_HG_{Hx}$

$x(1)=P_{4x}=[1\ 1\ 1\ 1]M_HG_{Hx}$

$x^`(t)=[3t^2\ 2t\ 1\ 0]M_HG_{Hx}$

t=0、1带入，得到其$R_{1x}、R_{4x}$约束

$x^`(0)=R_{1x}=[0\ 0\ 1\ 0]M_HG_{Hx}$

$x^`(1)=R_{4x}=[3\ 2\ 1\ 0]M_HG_{Hx}$

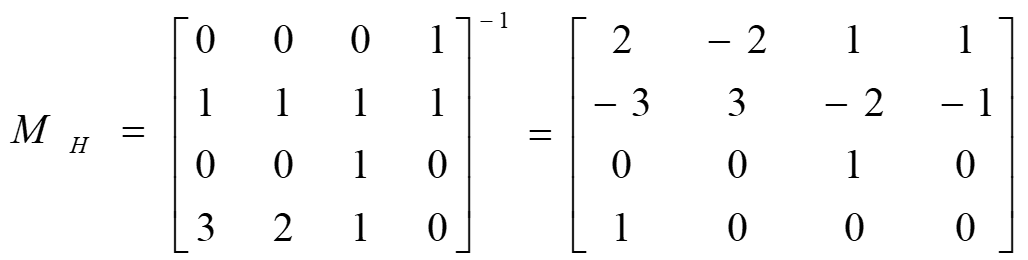
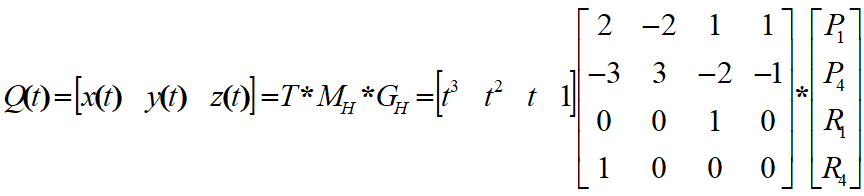
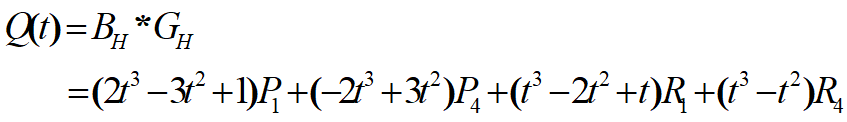
image-20230128180350806 image-20230128180400414 image-20230128180423807

Hermite 曲线完全插值控制点（2个，P1、P4）。两段Hermite曲线连接，可以轻易实现光滑连续。 切向量对曲线的影响如图

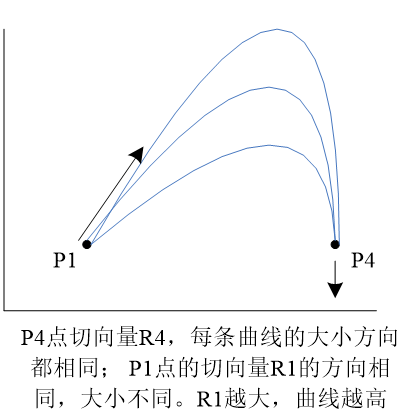
image-20230128180617230

习题：假定一条三次Hermite曲线的两个端点P1=<0,1>,P4=<3,0>,端点处切向量R1=<0,1>,R4=<-3,0>，请写出Hermite多项式形式，并绘出最后曲线，改变切向量，观察曲线形状变化。

Bezier曲线

对于三次Bezier曲线，给出4个型值点(控制点)，曲线的起点、终点（必须经过的点），另外两个型值点控制Bezier曲线在起点和终点之间的形状。

image-20230128181206198

通过给定两个不在曲线上的中间点来间接地确定端点切向量

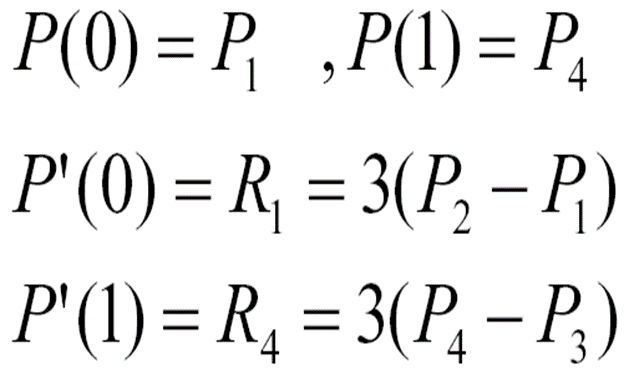
image-20230128181115001

可以导出Hermite几何向量与Bezier几何向量之间的关系：

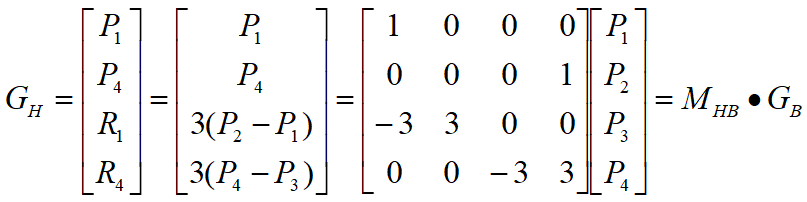
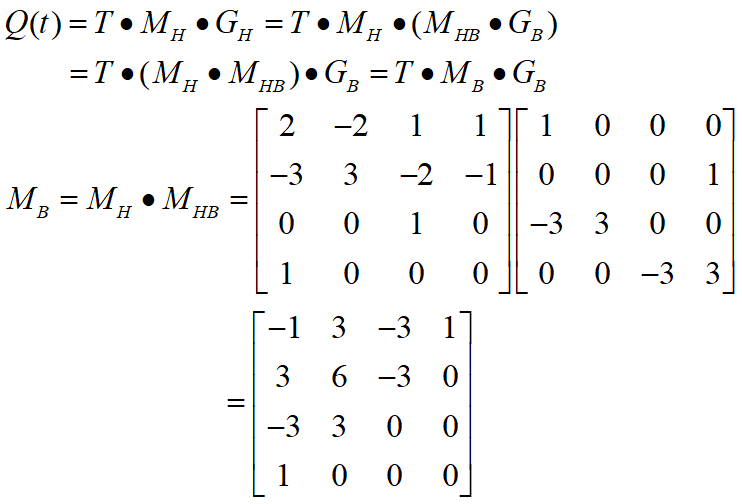
image-20230128181138690 image-20230128181338040

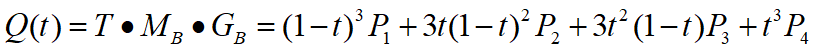
image-20230128181359593

Bezier曲线的性质：

  • R1和R4的大小及方向可以直接看出，便于控制曲线的形状。
  • 凸包(壳性：Bezier曲线一定在由P1P2P3P4四个端点确定的凸四边形(称为Bezier特征多边形）内（便于对曲线进行剪切）。
  • 对称性：n次Bezier曲线，如果端点不变，而将端点的次序颠倒，则曲线的走向相反，而形状保持不变。
  • 几何不变性：Bezier曲线的形状仅与Bezier特征多边形的各顶点的相对位置有关，而与坐标系的选择无关。

P3，P4，P5三点互异且共线就能保证两段Bezier曲线段光滑连接（G1连续），即：$P_4-P_3=k(P_5-P_4) k>0$。特别的，当k=1时，C1连续。

n阶Bezier曲线有一个统一的表达式，可以写作：

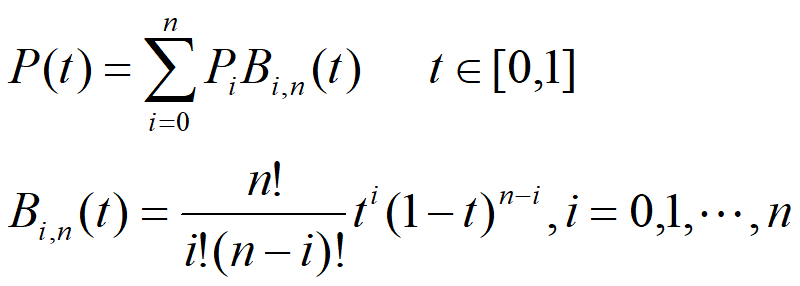
image-20230202175555632

练习：给定四个控制点P1(0,0,0)、P2(1, 1, 1)、P3(2,-1,-1)、P4(3,0,0)，构造Bezier曲线，并计算t = 0 , t = 1, t = 1/3，t= 2/3处的值。

B样条曲线

Bezier曲线有很多优点，例如Bezier曲线具有凸包性，容易改变形状（便于控制），容易做到C1、G1连续（外观性和直观性好），但是：Bezier曲线不具备局部可修改性。Bi,n(t)在（0，1）开区间内都都不为0，改变某一个特征点对整条曲线形状都有影响。

B样条通常用m +1个控制点，(P0、P1、…Pm)产生m-2个曲线段(Q3、Q4、…Qm)，m>=3，B样条曲线一般不过控制点。

若要产生封闭曲线，结尾处重复使用P0~P2。即P0 P1 P2…Pm P0 P1 P2.

B样条曲线

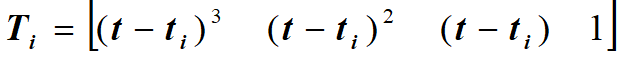
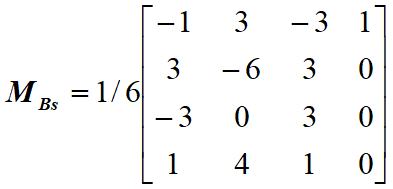
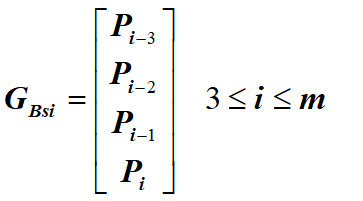
image-20230202180124323 image-20230202180129834 image-20230202180138334 image-20230202180135360

均匀B样条曲线

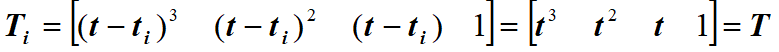
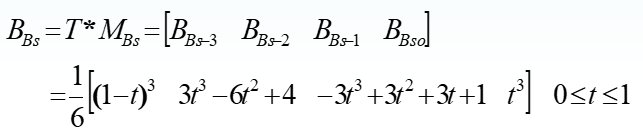
image-20230202181320079 image-20230202181346204

四点加权求和，调和函数非负且和为1 ，具有凸壳特性。

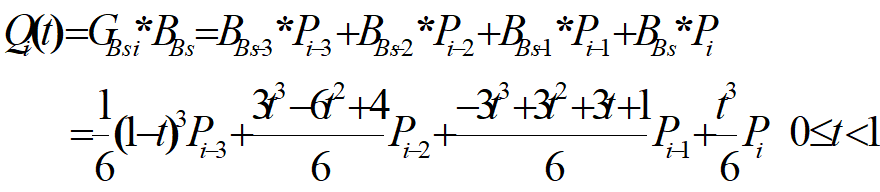
image-20230202181331490

B样条曲线的性质：

端点性质：对于Pi-3、Pi-2、Pi-1、Pi，4个端点，可生成靠近Pi-2、Pi-1两个型值点的一段B样条，再增加1个型值点，可利用Pi-2、Pi-1、Pi、Pi＋1，4个端点再产生一段B样条，依次类推可以生成整个3次B样条。

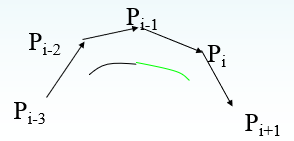
image-20230202184714094

B样条在连接点处的连续性

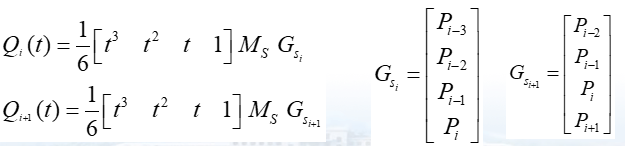
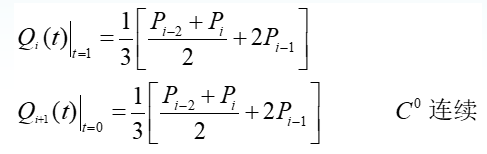
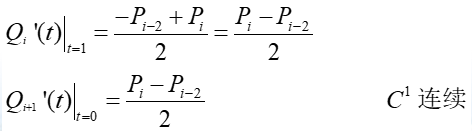
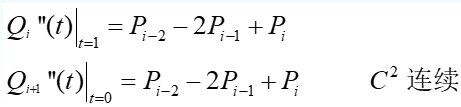
image-20230202184759869 image-20230202184810026 image-20230202184819092 image-20230202184859407

局部性：每一段B样条由4个控制点的位置矢量组成，改变其中的一个控制点，最多影响4条B样条曲线的位置，因此可对B样条曲线进行局部修改。

可扩展性：增加1个型值点（控制点），可再增加一段B样条，且新增加的B样条与原曲线在连接点处仍是C2连续。

三种曲线的比较与转换

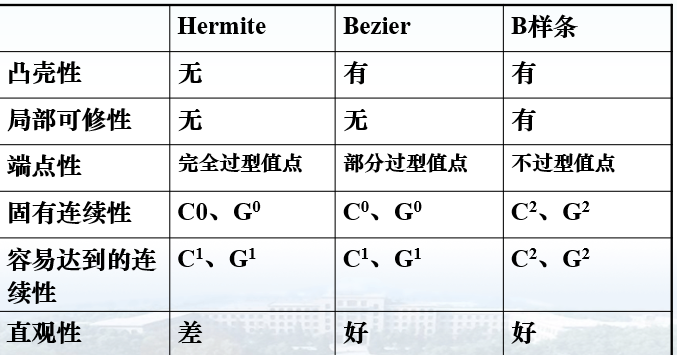
image-20230202185122591

在实际应用中，常常需要对三种曲线表示方法进行转换，而且这三种曲线表示方法之间也能够进行相互转换：

image-20230202185219319 image-20230202185224390