自适应遗传算法

对遗传算法的改进

在上面的文章中，我们介绍了遗传算法的具体实现内容，但是不可忽视的是，简单遗传算法由于遗传参数固定的特点，导致收敛速度慢，收敛精度差。所以我们不妨采用自适应遗传算法(Adaptive Genetic Algorithm, AGA)对遗传算法进行优化，通过遗传参数的自适应调整，可以让我们模拟出的生物种群在前期能够保持物种多样性，扩大搜索范围寻找潜在的全局最优解。而在后期生物种群接近最优解时，采用精英保留策略，保证其全局收敛[1,2]，防止破坏最优解，并且加快收敛速度。下面将介绍针对遗传算法自适应性的改进点。

阶段适应选择策略[1,2]

针对遗传算法的环境选择策略进行改进，使得遗传算法可以根据种群迭代时期的变化而选择不同的策略。假设最大进化代数为G，将整个进化过程划分成三个阶段。

第一阶段为[0, 0.382G)，这一阶段属于进化的初始阶段，模拟的是物种自由繁衍时期，不用考虑环境对生物种群的影响。为了能够使得生物种群更加多样，我们采用随机选择策略，让每个个体都有相同的机会被选中，在一定程度上减少遗漏，尽可能使得初始种群能够覆盖整个可行域，避免陷入局部最优解。

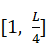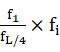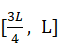第二阶段为[0.382G, 0.618G)，这一阶段开始出现个体的优劣差别，模拟的是物种开始受环境自然法则的影响，在优胜劣汰中继续繁衍。我们选择的策略对轮盘赌选择方法进行了优化。尽管轮盘随机的过程可以使得适应度高的个体被选中的概率大，但是由于过程是随机的，仍然有可能让好的个体丢失，而差的个体被保留。假设个体的总数为L，将个体按照适应度从高到底的顺序进行排序，将排好序的种群分成三类。取出前L/4和后L/4的个体，对其适应度进行适当的调整。对于的个体，适应度变化的公式为：，对于的个体，适应度变化的公式为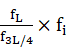：，而中间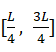的个体适应度不做调整。这样一方面能够让好个体的基因能够以更大的概率遗传下去，加快收敛速度。另一方面，对于中等个体，依然保留着较大遗传的可能性，具备着全局搜索潜在最优解的能力。

第三阶段为[0.618G，G]，这一阶段模拟的是物种生存的环境急剧恶化，对于不具备生存能力的个体将会被淘汰，而让好的个体基因保留，从而加快收敛的速度。于是我们选择在第二阶段改进适应度轮赌选择策略的基础上，加入精英保留策略，复制上一个阶段的得到最优解，并且淘汰新一代群体中适应度值最小的个体，从而使得群体个体总数保持不变。