CrossCBR问题解析
CrossCBR: Cross-view Contrastive Learning for Bundle Recommendation
一、标题:捆绑推荐中的跨视图对比学习
视图是如何体现“跨”字的,视图之间是怎样“对比”的
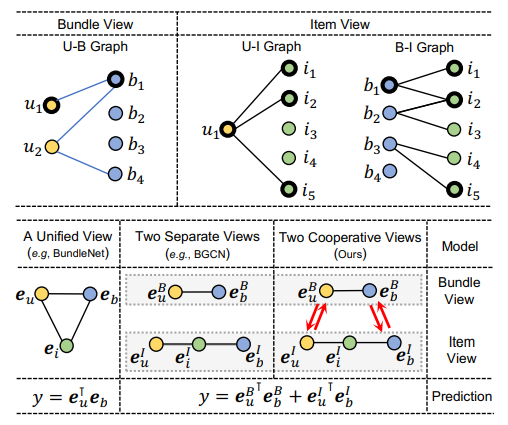
视图是如何体现“跨”字的
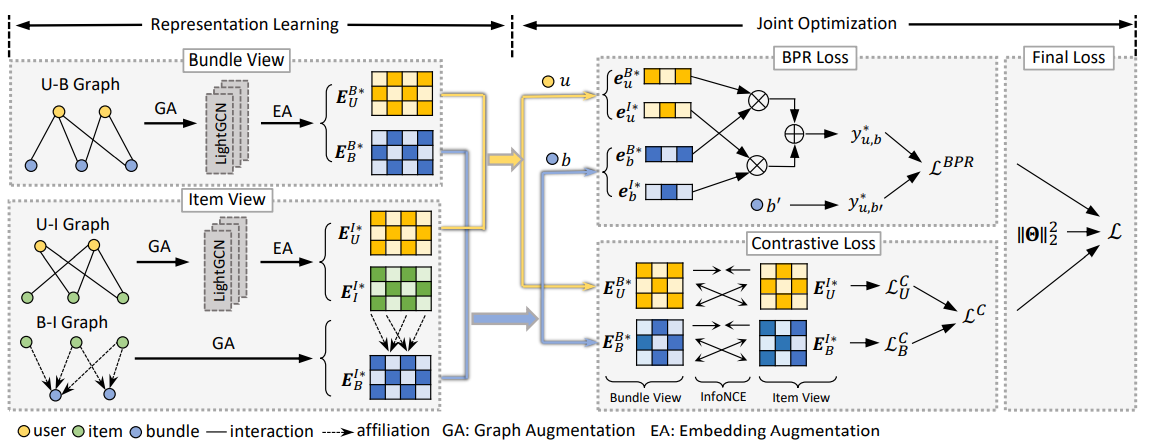
本文中含有两个视图,分别为包视图和物品视图
包视图直接通过用户-包图表的交互体现针对用户的捆绑包推荐
物品视图以物品作为粒度描述连接用户-物品图表和包-物品图表,间接描述用户对包偏好
最后得到模型预测表示为$y=e^{B^T}_ue^B_b+e^{I^T}_ue^I_b$
现有方法的不足
BundleNet算法盲目地将两个视图合并为一个统一的三方图,采用没有差异化的统⼀视图。无法从这两种视图中区分用户之间的行为相似性和包之间的内容关联性,从而模糊了它们之间的联系。
BGCN算法分别对包视图和物品视图执行表征学习和偏好预测,然后融合这两个特定于视图的预测。但它只考虑了预测级别的合作信号,而不是直接将这种信号插入到为推荐而优化的表征中。
视图之间是怎样“对比”的
在模型损失优化上,采用了InfoNCE对比损失和BPR loss(贝叶斯个性化排序损失),对比主要体现在InfoNCE对比损失上。
二、LightGCN
在NGCF上改进
在将用户和项目从ID嵌入成向量后,然后利用用户-项目二部图来进行传播,NGCF的传播算法如下
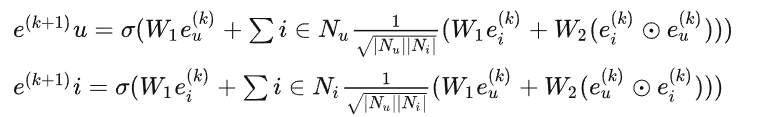
其中$e_u^{(k)}$和$e_i^{(k)}$分别表示在k层传播后用户u和项目i的嵌入,k表示传播的层数。$N_u$表示用户节点u交互过的邻域项目集,$N_i$表示项目节点i交互过的邻域用户集。σ表示非线性激活函数,W1和W2是训练的权重矩阵。
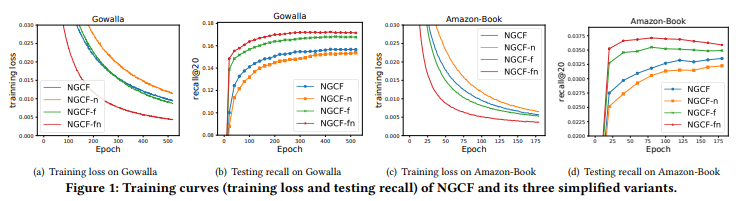
- NGCF-f,它删除了特征转换矩阵W1和W2。
- NGCF-n,它消除了非线性激活函数σ。
- NGCF-fn,它删除了两个特征转换矩阵和非线性激活函数。
可以看到NGCF-fn的召回率和loss都有明显改善。特征转换矩阵和非线性激活函数对最终结果影响不大,性能反而有所下降。
NGCF 是一个用于协同过滤的繁重的 GCN 模型,而GCN的基本思想是通过平滑图上的特征来学习节点的表示。 为了实现这一点,它迭代地执行图卷积,即,将邻居的特征聚合为目标节点的新表示。 这种邻域聚合可以抽象为:
$$
e_u^{(k+1)}=AGG(e_u^{(k)},e_i^{(k)}:i∈N_u)
$$
AGG是一个聚合函数(图形卷积的核心),它考虑了目标节点及其邻居节点的第k层表示形式。
很多工作将AGG特殊化,例如GIN 中的加权和聚合器,GraphSAGE中的LSTM聚合器和BGNN中的双线性交互聚合器等。
但是,大多数工作都将AGG函数与特征转换或非线性激活功能联系起来。 尽管它们在具有语义输入功特征的节点或图分类任务上表现良好,但是它们对于协作过滤可能很繁琐。
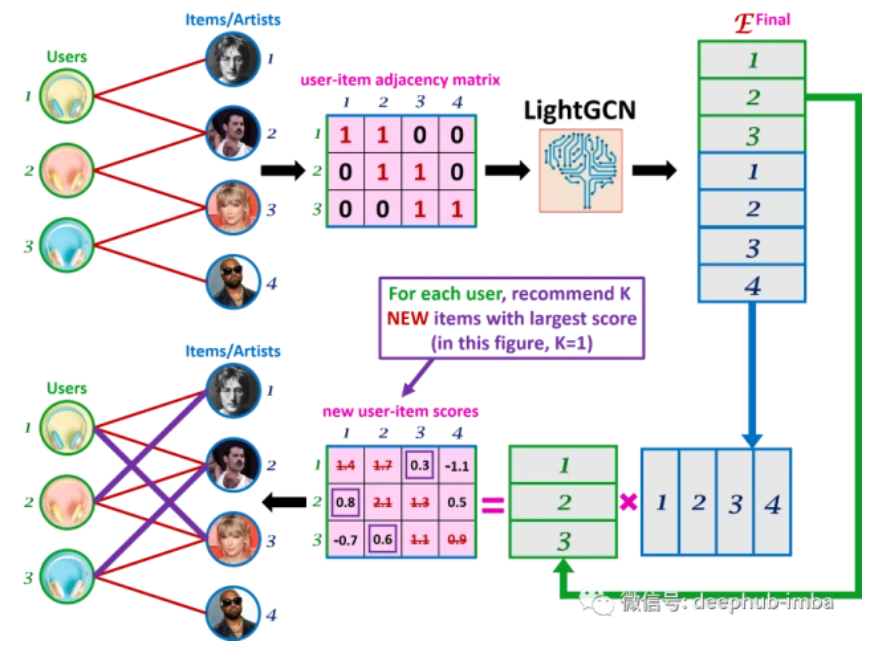
LightGCN模型图
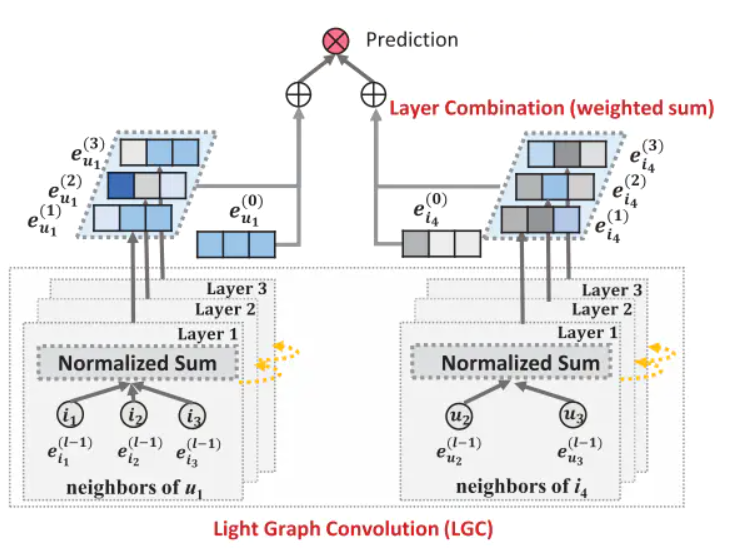
LightGCN模型的总体思路
(1)先将用户和项目节点的邻域聚合
(2)使用三层卷积层分别生成每层的嵌入
(3)将节点的原始输入与生成每层新的嵌入做一个加权和
(4)将用户和项目最终的生成节点表示做内积生成预测的分数
Light Graph Convolution轻型图卷积
LightGCN中,采用简单的加权和聚合器,放弃了特征变换和非线性激活的使用。只聚合已连接的邻居,而不集成目标节点本身(自连接)。LightGCN中的轻型图卷积运算(也称为传播规则)定义如下
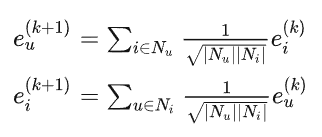
对称归一化项$\frac{1}{\sqrt{|N_u|}\sqrt{|N_i|}}$遵循标准GCN的设计,可以避免嵌入的规模随着图卷积操作的增加而增加。
层组合和模型预测
在LGCN中,唯一可训练的模型参数就是第0层的嵌入,即为所有用户的$e^{(0)}_{u}$和所有项的$e^{(0)}_i$。当第0层被给定后,通过轻量图卷积公式计算高层嵌入。在k层LGC之后,我们进一步组合在每个层上获得的嵌入,以形成用户(项)的最终表示。
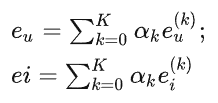
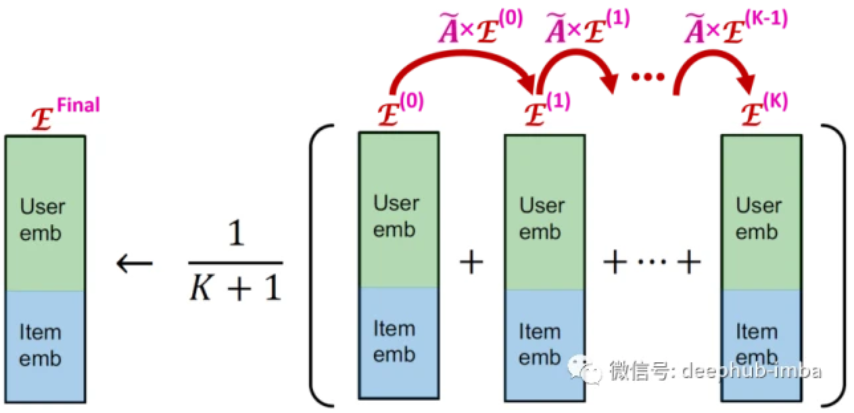
其中,$α_k≥0$表示第k层嵌入在构成最终嵌入中的重要度。可以将其视为要调整优化的超参数,发现将$α_k$统一设置为$\frac{1}{K+1}$通常可获得良好的性能,使其保持简单性。
采用图层组合的原因
(1)随着层数的增加,嵌入会变得更加平滑。因此,仅使用最后一层是有问题的。
(2)不同层的嵌入具有不同的语义。 例如,第一层对具有交互作用的用户和项目强制执行平滑操作,第二层对在交互的项(用户)上重叠的用户(项目)进行平滑操作,更高的层则捕获较高级别的邻近度。因此,将它们结合起来将使表示更加全面。
(3)将不同层的嵌入与加权和结合起来,可以捕获图卷积和自连接的效果。
模型预测定义为用户和项目最终表示的内积,作为推荐生成的排名:
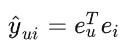
矩阵形式:
令用户-项目交互矩阵为$R=R^{M×N}$,其中M,N分别表示用户和物品的数量。如果u与i交互,则每个项(entry) $R_{ui}$为 1,否则为0。然后我们得到用户-项目邻接矩阵为:
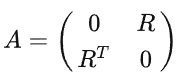
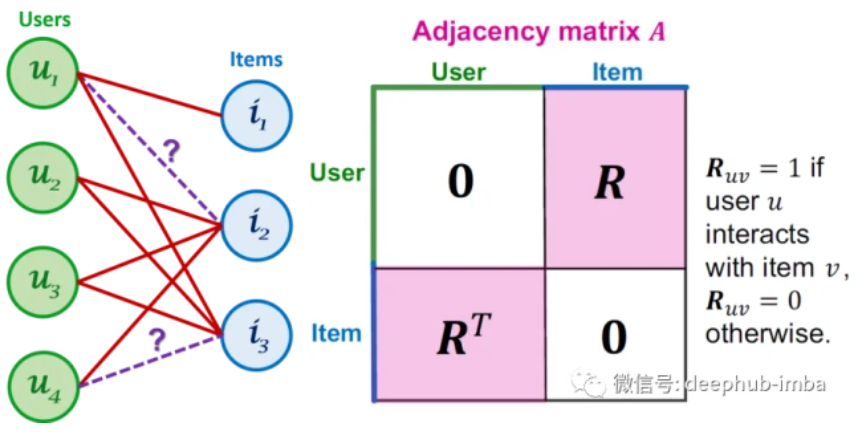
令第0层的嵌入矩阵为$E^{(0)}∈R^{(M+N)T}$,T为嵌入大小
$$
E^{(k+1)} = (D^{−\frac{1}{2}}AD^{−\frac{1}{2}})E^{(k)}
$$
D为(M+N)(M+N)维矩阵,其中$D_{ii}$的值为邻接矩阵A(也称为度矩阵)的第i行向量中的非零项的数目。其中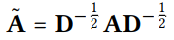 为归一化矩阵。
为归一化矩阵。
最后,我们得到用于模型预测的最终嵌入矩阵为:
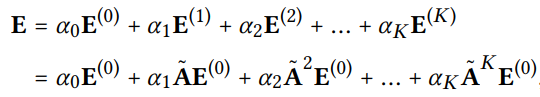
α是学习层组合系数
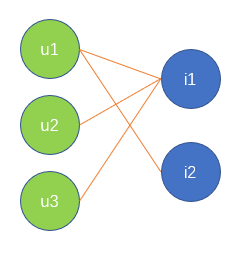
我们以下图的用户-物品交互图为例
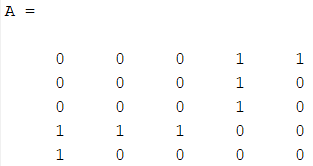
根据构造规则,得到用户-项目邻接矩阵A为
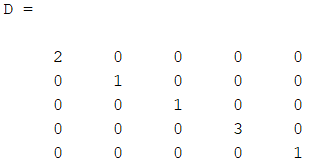
根据A中每行非零项的数目,得到矩阵D为
则归一化矩阵
为
(目前还不会将矩阵形式和图卷积运算联系起来)
三、InfoNCE loss对比损失
对比学习损失函数有多种,其中比较常用的一种是InfoNCE loss。
InfoNCE loss公式
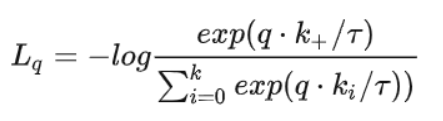
其中的q和k可以表示为其他的形式,比如相似度度量,余弦相似度等。分子部分表示正例之间的相似度,分母表示正例与负例之间的相似度,因此,相同类别相似度越大,不同类别相似度越小,损失就会越小。
与交叉熵损失对比
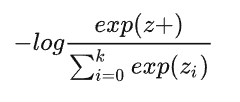
上式中的k在有监督学习里指的是数据集的总类别数,如CV的ImageNet数据集有1000类,k就是1000。但如果通过使用数据增强手段产生对比学习正样本对,有多少张图就有多少类,会导致计算复杂度非常高。
而在对比学习InfoNCE loss里,这个k指的是负样本的数量。InfoNCE loss公式分母中的sum是在1个正样本和k个负样本上做的,从0到k,所以共k+1个样本,
对NCE Loss对比
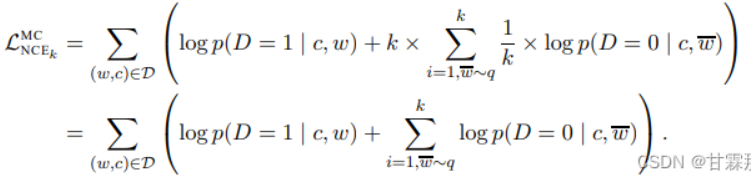
InfoNCE loss是基于对比度的一个损失函数,是由NCE Loss损失函数演变而来。NCE Loss损失函数是基于采样的方法,将多分类问题转为二分类问题,分为数据类别和噪声类别。正样本标值为1,负样本标值为0。 Info NCE loss作为NCE的一个简单变体,演变成一个多分类问题。
理解
论文MoCo提出,我们可以把对比学习看成是一个字典查询的任务,即训练一个编码器从而去做字典查询的任务。假设已经有一个编码好的query q(一个特征),以及一系列编码好的样本k0,k1,k2,…,那么k0,k1,k2,…可以看作是字典里的key。假设字典里只有一个key即k+(称为k positive)是跟q是匹配的,那么q和k+就互为正样本对,其余的key为q的负样本。一旦定义好了正负样本对,就需要一个对比学习的损失函数来指导模型来进行学习。这个损失函数需要满足这些要求,即当query q和唯一的正样本k+相似,并且和其他所有负样本key都不相似的时候,这个loss的值应该比较低。反之,如果q和k+不相似,或者q和其他负样本的key相似了,那么loss就应该大,从而惩罚模型,促使模型进行参数更新。
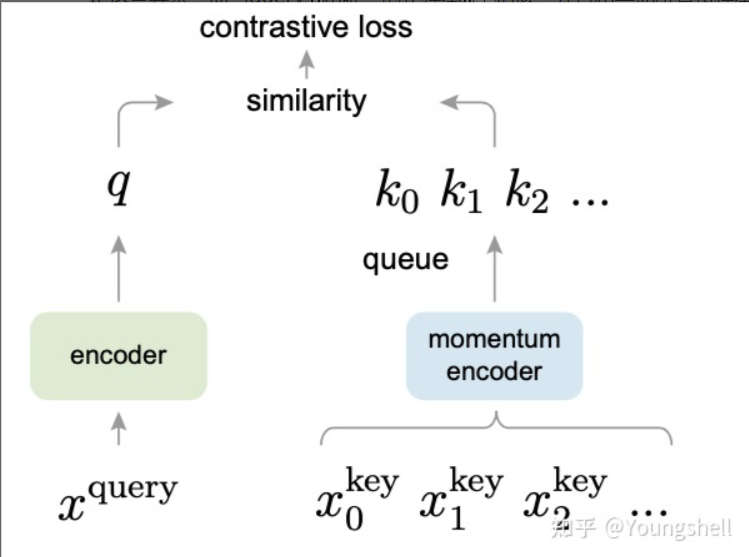
一个好的对比学习应该具备以下两个属性:Alignment和Uniformity。
Alignment(对齐)指的是相似的例子,也就是正例,映射到单位超球面后,应该具有比较接近的特征,球面距离应该比较近;
Uniformity(均匀性)指的是系统应该倾向于应该在特征里保留尽可能多的信息,映射到球面上就要求,单位球面上的特征应该尽可能地均与分布在球面上,分布越均匀,意味着保留的特征也就越多越充分。因为,分布越均匀,意味着各自保留各自的独有的特征,这代表着信息保留越充分。
Uniformity特性的极端反例,所有数据都映射到单位超球面的同一个点上,这代表着所有数据的信息都被丢掉,体现为数据分布极度不均匀得到了超球面上的同一个点。也就意味着,所有数据经过两次非线性计算之后都收敛到同一个常数上,这种异常情况我们称之为:模型坍塌(collapse),如下图所示。
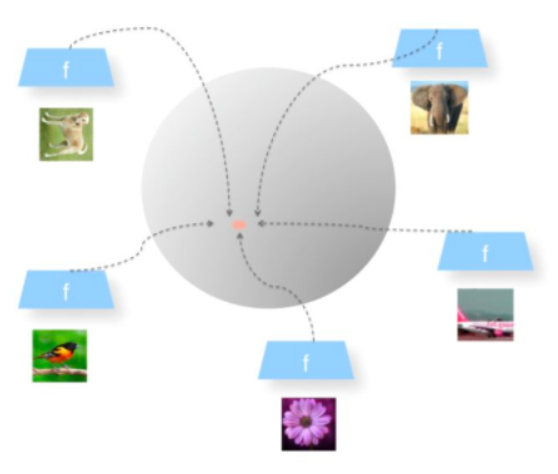
在公式中可知,分子中的S()体现出了Alignment属性,它期望在超球面上正例之间的距离越近越好;分母中的S()则体现了Uniformity属性,它期望在负例对之间的距离尽可能的远,这种推力会尽量将点尽可能地均匀分布在超球面上,保留了尽可能多的有用信息。损失函数inforNCE会在Alignment和Uniformity之间寻找折中点。如果只有Alignment模型会很快坍塌到常数,所以损失函数中采用负例的对比学习计算方法,主要是靠负例的Uniformity来防止模型坍塌。
温度系数τ
温度系数τ针对负例难度。在对比学习中,对于数据x,除了他的唯一正例x+外,所有其他的数据都是负例。这些负例有一些和x比较像,有一些差异比较大,对于比较接近原始数据特征,导致区分难度比较大。会导致比较像的、有难度的负例在超球面上距离比较近,比较容易区分的在超球面上距离比较远。
温度参数T起到的作用:温度参数会将模型更新的重点,聚焦到有难度的负例,并对他们做相应的惩罚,难度越大,也即与x越接近,分配到的惩罚系数越多。所谓惩罚就是,就是在模型优化的过程中,距离越近的负例易获得更多的权重,会具有更大的斥力将其推远。
温度系数是设定的超参数,它的作用是控制模型对负样本的区分度。温度系数设的越大,q*k的分布变得越平滑,那么对比损失会对所有的负样本一视同仁,导致模型学习没有轻重。如果温度系数设的过小,则模型会越关注特别困难的负样本,但其实那些负样本很可能是潜在的正样本,这样会导致模型很难收敛或者泛化能力差。因此温度系数的设定是不可或缺的。
四、BPR loss贝叶斯个性化排序损失
设计这个损失函数的最主要的目标是:未来正边的计分函数结果是一个较大的数字,而未来负边的计分函数结果是一个较小的数字。所以结合这两个问题的一个比较好的方法是:希望用户u的给定未来正边和用户u的给定未来负边之间的差值是一个较大的数字:
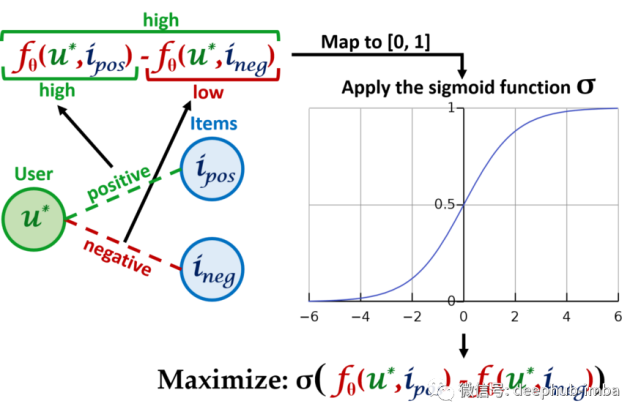
在使用 sigmoid 函数将两个分数的差异映射到区间 [0, 1]后,就能够将分数视为概率。因此对于一个给定用户u,可以将给定的所有正边和负边对的分数组合起来输入损失函数中。然后在所有用户中平均这些损失以获得最终的损失,这称为贝叶斯个性化排名 (Bayesian Personalized Ranking BPR) 损失
排序推荐算法背景
排序推荐算法历史很悠久,早在做信息检索的各种产品中就已经在使用了。
最早的第一类排序算法类别是点对方法(Pointwise Approach),这类算法将排序问题被转化为分类、回归之类的问题,并使用现有分类、回归等方法进行实现。
第二类排序算法是成对方法(Pairwise Approach),在序列方法中,排序被转化为对序列分类或对序列回归。所谓的pair就是成对的排序,比如(a,b)一组表明a比b排的靠前。我们要讲到的BPR就属于这一类。
第三类排序算法是列表方法(Listwise Approach),它采用更加直接的方法对排序问题进行了处理。它在学习和预测过程中都将排序列表作为一个样本。排序的组结构被保持。
BPR建模思路
在BPR算法中,我们将任意用户u对应的物品进行标记,如果用户u在同时有物品i和j的时候点击了i,那么我们就得到了一个三元组$<u,i,j><u,i,j>$,它表示对用户u来说,i的排序要比j靠前。如果对于用户u来说我们有m组这样的反馈,那么我们就可以得到m组用户u对应的训练样本。
既然是基于贝叶斯,那么我们也就有假设,这里的假设有两个:一是每个用户之间的偏好行为相互独立,即用户u在商品i和j之间的偏好和其他用户无关。二是同一用户对不同物品的偏序相互独立,也就是用户u在商品i和j之间的偏好和其他的商品无关。为了便于表述,我们用>u>u符号表示用户u的偏好,上面的<u,i,j><u,i,j>可以表示为:$i>_uj$。
在BPR中,这个排序关系符号>u>u满足完全性,反对称性和传递性,即对于用户集U和物品集I:
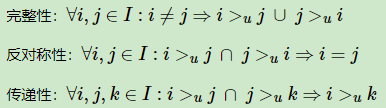
同时,BPR也用了和funkSVD类似的矩阵分解模型,这里BPR对于用户集U和物品集I的对应的U×I的预测排序矩阵$X^¯$,我们期望得到两个分解后的用户矩阵W(|U|×k)和物品矩阵H(|I|×k),满足
$$
X^¯=WH^T
$$
这里的k和funkSVD类似,也是自己定义的,一般远远小于|U|,|I|。由于BPR是基于用户维度的,所以对于任意一个用户u,对应的任意一个物品i我们期望有:
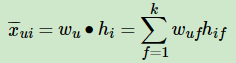
BPR公式
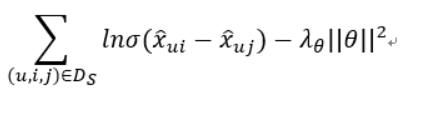
五、Data augmentation数据增强
六、模型图分析