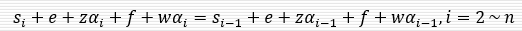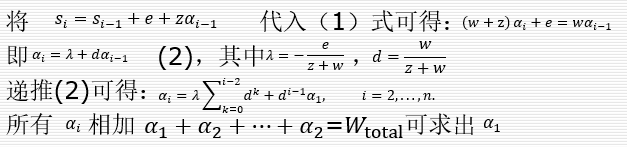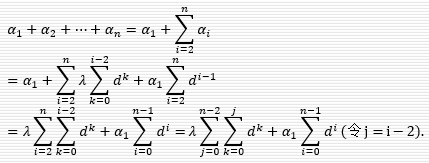大数据优化建模与算法笔记
第一章
1.1 运输问题与方程组求解的优化建模
问题1.运输问题
生产一种产品,有m个产地,n个销售地,从第i个产地运输单位产品到第j个销售地的运费为$c_{𝑖𝑗}$,第i个产地产量为$a_i$,第j个销售地的需要量是$b_j$。假设产销平衡(生产多少,销售多少),从第i个产地运到第j个销售地的运量为$x_{ij}$,问怎么制定运输方案,才能使运费最少?
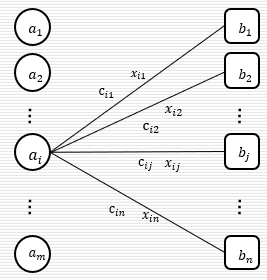
目标函数为
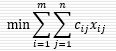
约束条件为
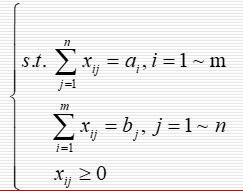
整体模型为
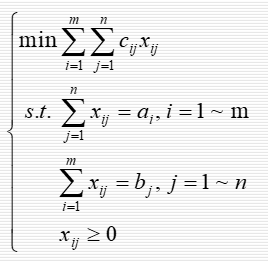
课外作业


1.2 同构网络可分任务调度问题的优化建模
问题描述
设有N+1台处理机通过星型网络互连,如图1所示,其中$P_0$为主处理机,其余为从处理机,主处理机只负责数据的切分和传输,从处理机负责数据的处理。$l_i$是链接$P_0$和$P_i$的通信链路。从处理机的能力一样,称为同构网络。不妨记 $P_1,P_2,…,P_N$为主处理机给从处理机传输数据的调度顺序。
$P_0$将大小为$W_{total}$的数据切分为N个子块(任务)并传输给$P_1,P_2,…,P_N$,$P_0$同一时刻只能给一个从处理机$P_i$传输任务,$P_i$只有在完全接收子任务后才开始处理该任务。并不要求所有的处理机都必须参与处理任务。
令z表示从$P_0$传输单位数据到$P_i$所需要的时间,则传输大小为$α_i$的数据所需的时间为$zα_i$;令w表示处理机$P_i$处理单位数据的时间,则处理$α_i$的时间为$wα_i$。由于考虑启动开销,所以子任务$α_i$的传输时间和处理时间分别为:$e+zα_i$和$f+wα_i$,其中e和f分别表示传输启动开销和处理启动开销。
优化目标:
1)确定参与处理数据的从处理机最优数目
2)最优的任务分配方案使得处理完所有任务所用时间最短最短。
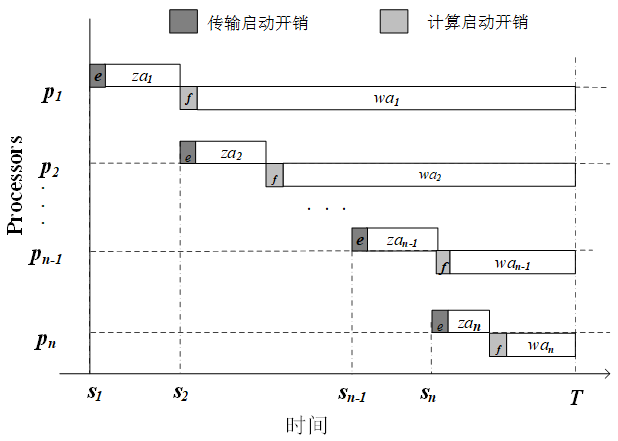
记处理机$P_i$开始接受任务的时刻为$s_i$,所以对于处理机$P_1$有$s_1=0$。处理机$P_i$的开始时间$s_i$与前一个处理机$P_{i-1}$的开始时间$s_{i-1}$以及$P_{i-1}$接受子任务$α_{i-1}$的传输时间$e+zα_{i-1}$有关:$s_i=s_{i-1}+e+zα_{i-1}$,处理完所有任务所需时间为:
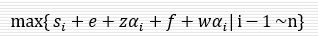
则最短时间为
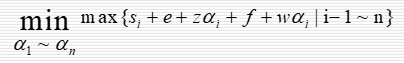
已有研究证明了只有当所有处理机同时完成处理任务时,任务的完成时间最短,否则完全可以将后完成任务的处理机上的部分数据分配给先完成任务的处理机上执行。由所有处理机同时完成计算可以得到下面的等式: