神经网络学习笔记
神经网络 第一章 人工神经网络绪论
1.1人工智能的含义
对人工智能的研究必然借鉴自然智能—人脑的研究成果,根据侧重点的不同,可分为三大类:
结构模拟:神经计算,生理学派,连接主义
生理学派
- 根据人脑的生理结构和工作机理,实现计算机的智能,是一种局部和近似的模拟(ANN)
特点:
- 利用NN的自学习能力获取知识,再利用知识解决问题
- 具有高度的并行性、分布性、很强的鲁棒性和容错性
- 擅长模拟人脑的形象思维,便于实现人脑的低级感知功能:图象、语音的识别和处理
功能模拟:符号推演,心理学派,符号主义
- 心理学派
- 根据人脑的心理模型,将知识/问题表示成某种逻辑网络,采用符号推演的方法,实现搜索、 推理、学习等功能。如自动机器推理、定理证明、专家系统、机器博弈等
- 擅长模拟人脑的逻辑思维,便于实现人脑的高 级认知功能(推理、决策等)
- 心理学派
行为模拟:控制进化,控制论学派,行为主义,进化主义
- 控制论学派
- 基于“感知—行为模型” ,模拟人在控制过程中的智能活动和行为特征:自优化、自适应、自学习、自组织等
- 也可称为现场AI(Situated AI),强调智能系统与环境的交互
- 认为智能取决于感知和行动,智能行为不需要知识,认为人的智能、机器的智能可以逐步进化, 但必须与现实交互
- 控制论学派
1.3人工神经网络的概念
Artificial Neural Networks,简记作ANN
传统的AI技术模拟左脑的逻辑思维
ANN技术模拟右脑的形象思维
人工神经网络是受生物大脑启发,基于模拟生物大脑的结构和功能,采用数学和物理方法进行研究而构成的一种信息处理系统。它是由许多非常简单的并行工作的处理单元按照某种方法相互连接,并依靠其状态对外部输入信息进 行动态响应的计算机系统。
大脑是由大量神经细胞或神经元组成的,每个神经元可以被看作是一个小的处理单元,这些神经元按照某种方式互相连接起来,形成大脑内部的生物神经元网络,这些神经元又随着所接收到的多个激励信号的综合大小而呈现兴奋或抑制状态。
大脑的学习过程就是神经元之间连接强度随外部激励信息做自适应变化的过程,而大脑处理信息的结果则由神经元的状态表现出来。
并行、分布处理结构
一个处理单元的输出可以被任意分枝,且大小不变
输出信号可以是任意的数学模型
处理单元完全的局部操作

1.4人工神经网络的特点
固有的并行结构和并行处理特性
ANN的计算功能分布在多个处理单元上,在同一层内的处理单元同时并行操作。ANN中的信息处理是在大量单元中并行而又分层进行的。
知识的分布存储特点
在ANN中,知识不是存储在特定的存储单元中, 而是分布存储在整个网络的所有连接权中。
良好的容错特性
当输入是一些模糊、变形等不完善的数据和信息时,ANN能够通过联想恢复完整的记忆,从而实现对不完整输入信息的正确识别。
高度非线性及计算的非精确性
ANN的结构的并行性和知识的分布存储使其信息的存储与处理表现出了空间上分布,时间上并行的特点,使得网络非线性。
由于能够处理一些不精确、不完整的模糊信息, 所以解为满意解而非精确解。
自学习、自组织和自适应性
自学习是指当外部环境发生变化时,经过一段时间的训练或感知,神经网络能够对给定的输 入产生期望的输出。
自组织是神经网络通过训练可以自行调节连接权值,即调节神经元之间的突触连接,使其具有可塑性,以逐步构建适应于不同信息处理要求的神经网络。
联想记忆
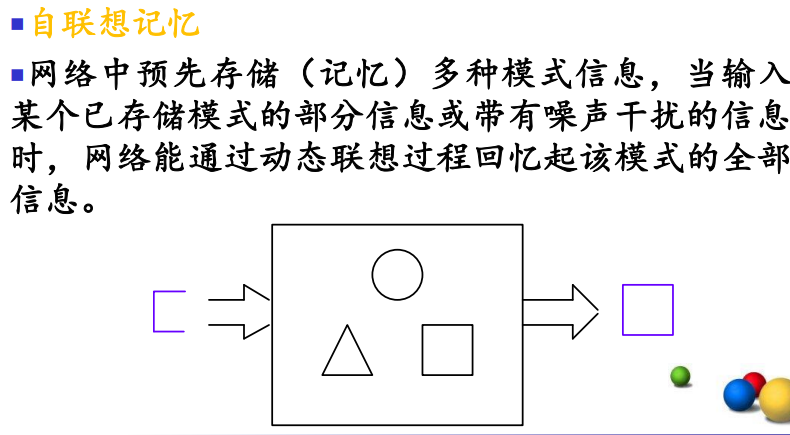
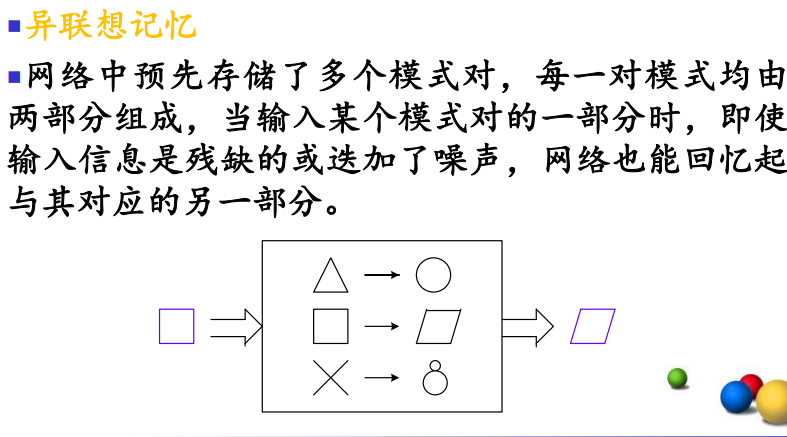
1.6 ANN的应用领域
从样例中学习
文字处理
生物特征识别
生物医学
遥感
文档分类
预测决策
机器人
1.7 ANN面临的主要挑战

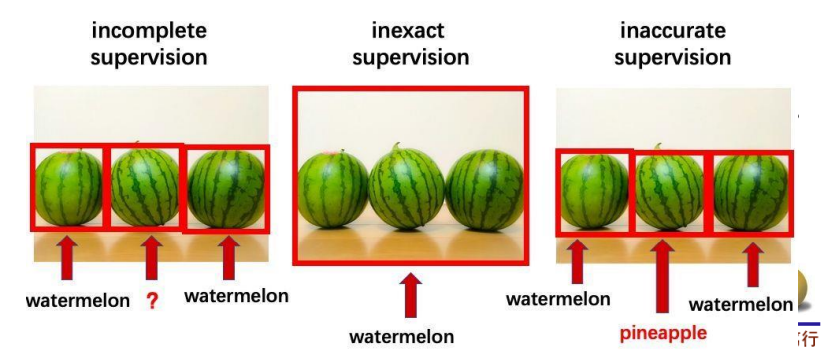
不确切监督:任务力度需要很细,但是输入标签比较粗。比如任务需要语义分割,但是给的标签为点标注或线标注
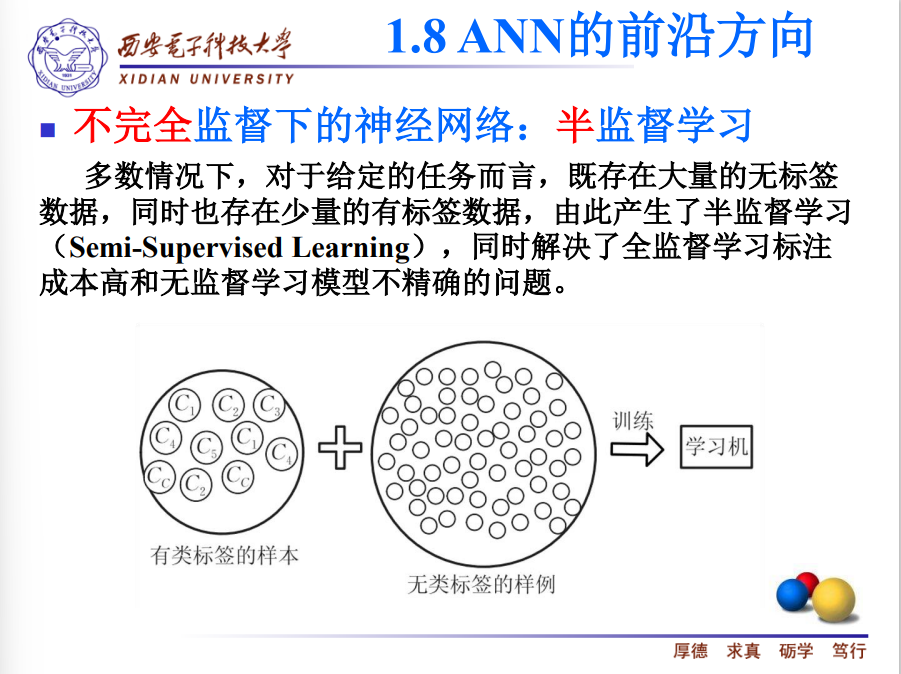
1.8ANN的前沿方向
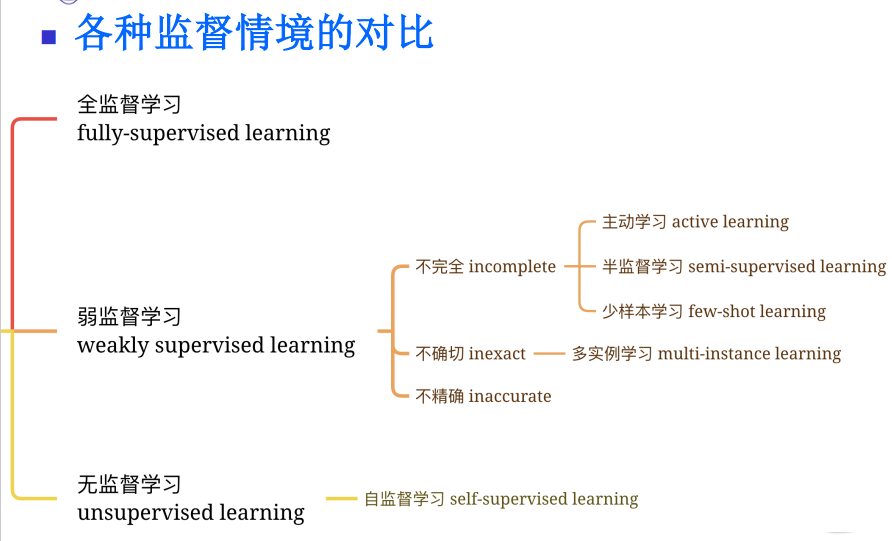
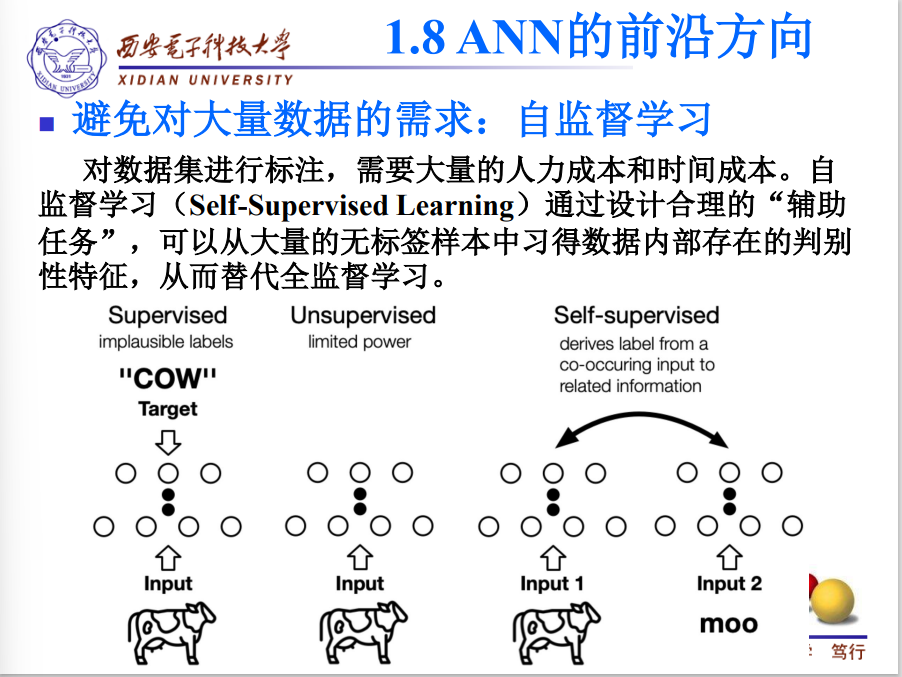


图像分类
点标注
目标识别
线标注
语义分割

Chapter 2 Artificial Neural Network
认知计算:基本神经信息处理机制
- Vision视觉:CNN图片处理
- Attention注意力:attention mechanism权重
- Dopamine and Reward多巴胺:奖惩,强化学习
- Memory记忆:RNN时间序列
- Meaning意义
- Task directed behavior任务导向型:adversarial生成对抗学习,feature特征解耦学习
神经元
- 树突:接收
- 轴突:发射
- 突触:设定阈值(兴奋、抑制)
- 胞体:对输入信号求和
人工神经元
- Node:节点
- Input:输入
- Output:输出
- bias:偏置
- activation:激活函数
- weight:权重
激活函数
阶跃函数
二分类

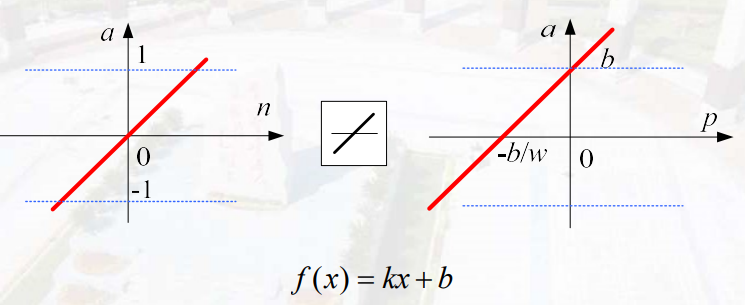
线性函数
分类具有线性特点,无法处理非线性问题
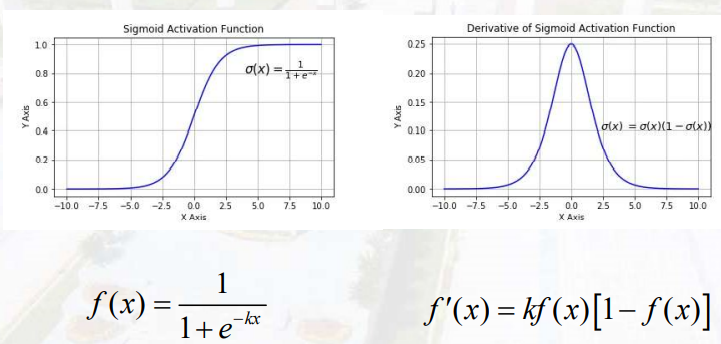
sigmod
用于转化线性至非线性,导数便于计算
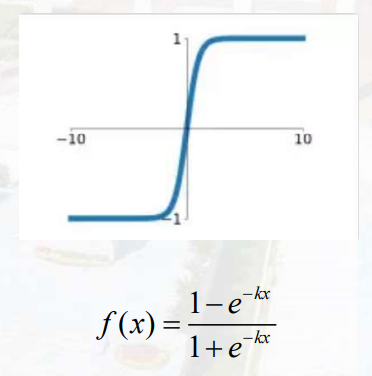
tanh
线性转非线性,将输出值固定在一个区间。梯度爆炸消失,计算量较大
leaky relu
relu函数 f(x)=max(0, x)
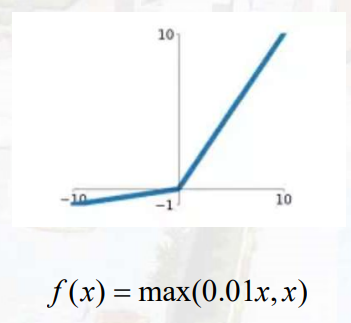
Chapter 3 Learning & Perceptron
输入层——隐藏层——输出层
信号逐层传递,同层之间无联系
使用$w_{x,y}$表示权重,其中x为后层编号,y为前层编号
损失函数(单个样例的误差)
0-1损失
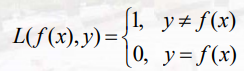
平方损失
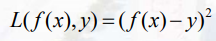
绝对值损失
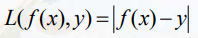
代价函数(训练样本集的平均误差)
均方误差
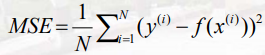
平均绝对误差
通常用于回归
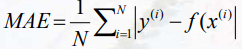
交叉熵代价函数(看录播)
通常用于分类

真实概率分布和预测概率分布尽可能相似接近
Rosenblatt Perceptron算法
采用阶跃激活(-1,1)
- Input:${(X_i,Y_i)}_{i=1\sim n}$
- Random:(w, b)
- Pick up :$X_i$
- 如果wx+b≥0且y=-1,即y(wx+b)<0,则$W=W+\eta yX$,$b=b+\eta y$
- repeat stet(3),直到所有的归类均正确





学习(看录播)
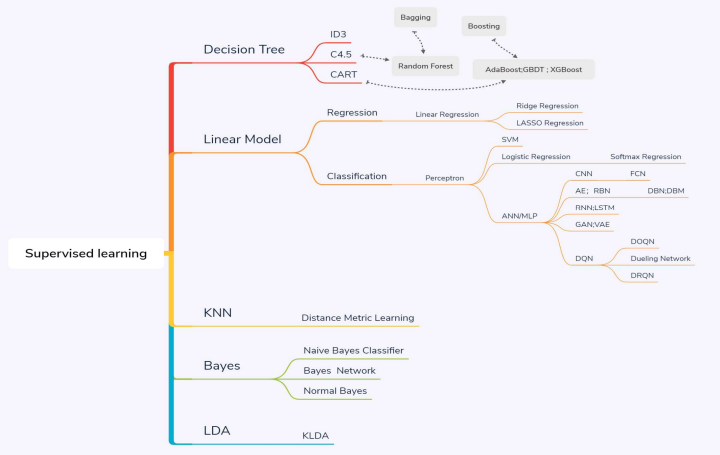
有监督学习
方法:回归和分类
给出样本的标准答案,以答案为导向
无监督学习
方法:聚类
以相似性为导向
误差为样本集到中心点的距离:欧氏距离,余弦相似度。
强化学习
R and P奖惩机制

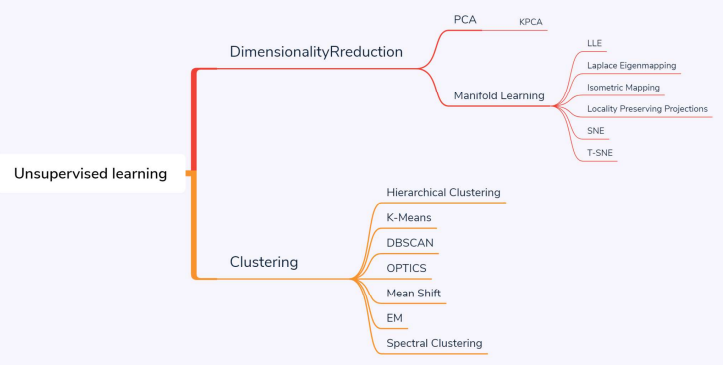
Chapter 4 Optimization优化
梯度

梯度下降法
选择初始点$x_0$,迭代直到收敛
$x_{t+1}=x_t-\eta \nabla f(x_t)$,其中$\eta$为学习率
可能的停止条件:迭代到$||\nabla f(x_t)||≤ \epsilon$,其中$\epsilon>0$
学习率过大可能会跳过极小点,学习率过小会导致收敛太慢,前大后小。
SGD随机梯度下降
随机梯度下降法(Stochastic Gradient Descent, SGD)
随机梯度下降算法每次从训练集中随机选择一个样本来进行学习(batch_size=1)。
优点:每次只随机选择一个样本来更新模型参数,因此每次的学习是非常快速的,并且可以进行在线更新。
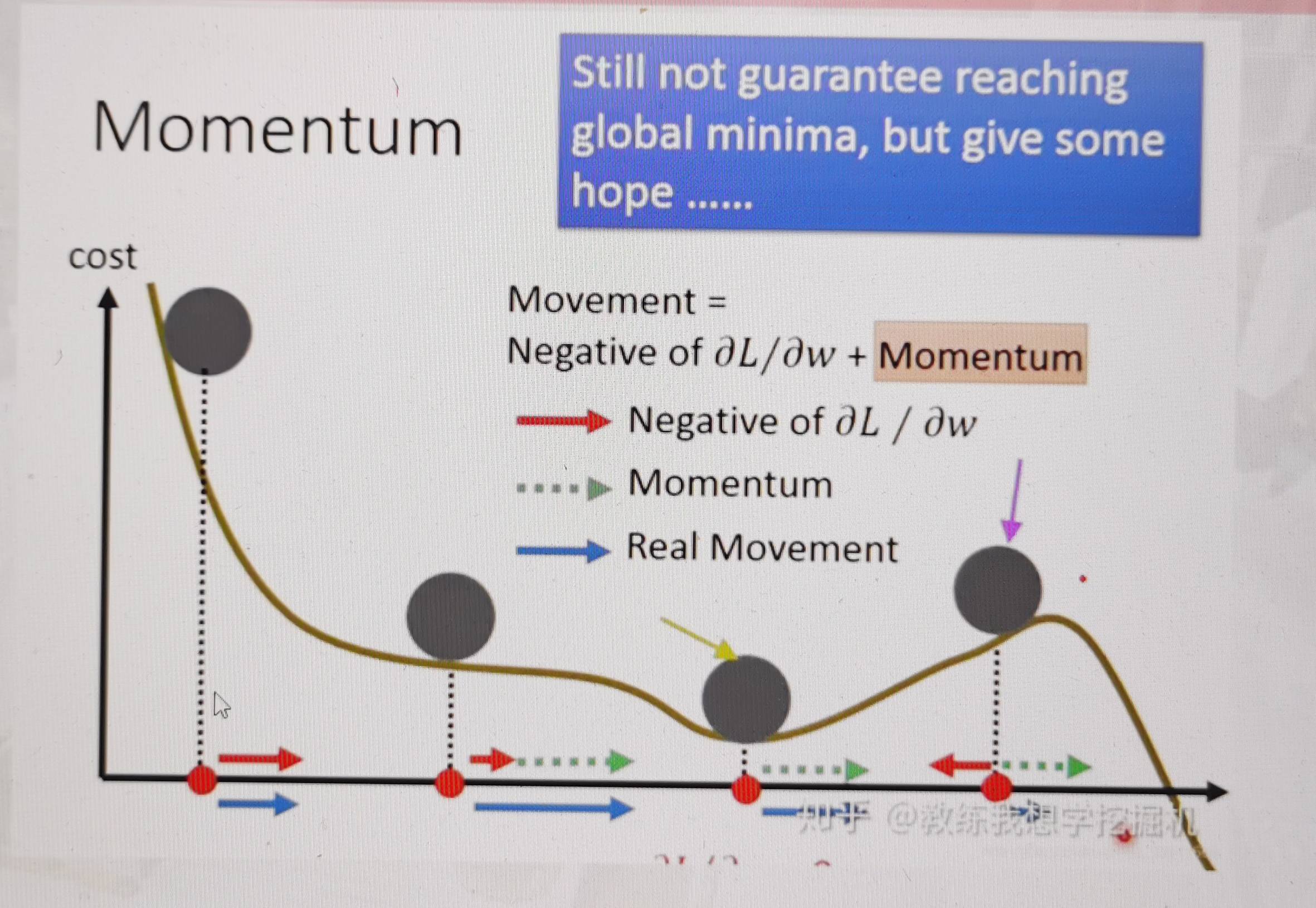
SGD波动带来的好处,在类似盆地区域,即很多局部极小值点,那么这个波动的特点可能会使得优化的方向从当前的局部极小值点调到另一个更好的局限极小值点,这样便可能对于非凹函数,最终收敛于一个较好的局部极值点,甚至全局极值点。
缺点:每次更新可能并不会按照正确的方向进行,因此会带来优化波动,使得迭代次数增多,即收敛速度变慢。
批量梯度下降法(Batch Gradient Gradient Descent, BGD)
每次使用全部的训练样本来更新模型参数/学习
优点:每次更新都会朝着正确的方向进行,最后能够保证收敛于极值点
缺点:每次学习时间过长,并且如果训练集很大以至于需要消耗大量的内存,不能进行在线模型参数更新。
小批量梯度下降法(Mini-batch Gradient Descent, SGD)
小批量梯度下降综合了batch梯度下降与stochastic梯度下降,在每次更新速度与更新次数中间实现一个平衡,其每次更新从训练集中随机选择k(k<m)个样本进行学习。
优点:
- 相对于随机梯度下降,Mini-batch梯度下降降低了收敛波动性,即降低了参数更新的方差,使得更新更加稳定
- 相对于批量梯度下降,其提高了每次学习的速度;
- MBGD不用担心内存瓶颈从而可以利用矩阵运算进行高效计算
优化类别

反向传播算法
首先正向计算误差值,再反向调整权重值
计算误差,对权重求偏导,找到误差减小最快方向。
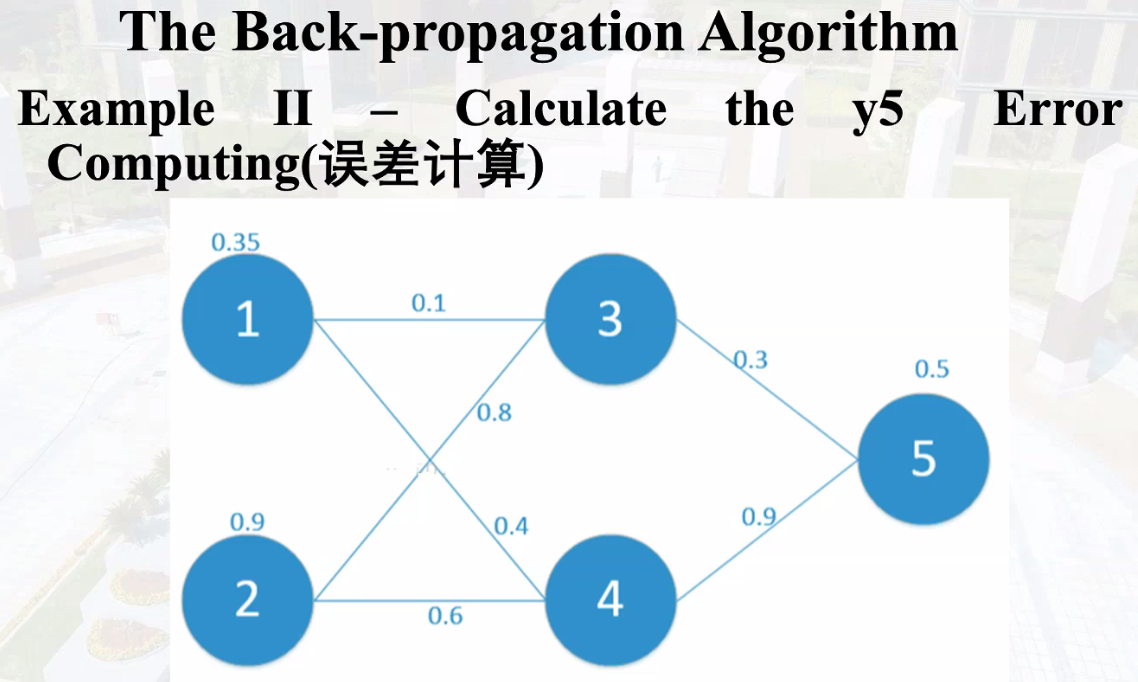
结点i的输入为$z_i$,结点i的输出为$y_i$
损失函数为$E=\frac{1}{2}(y_p-y_a)^2$,激活函数为$f(x)=\frac{1}{1+e^{-x}}$
则计算y5误差的计算过程为
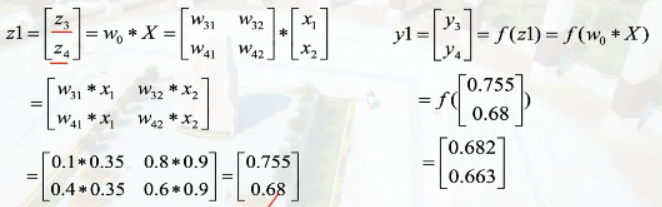
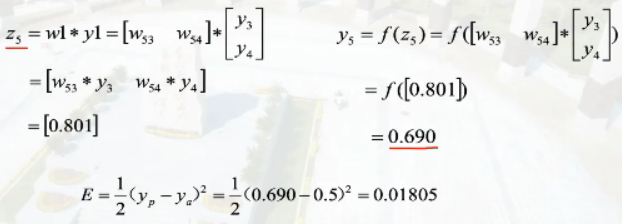
利用链式法则求$W_{53}$的偏导,从而对$w_{53}$进行权值修正,根据前向计算的公式,有
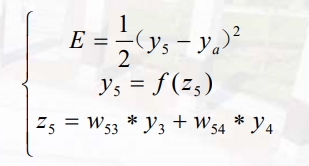
$$
\Delta w_{53}=\frac{\delta E}{\delta w_{53}}=\frac{\delta E}{\delta y_5}\frac{\delta y_5}{\delta z_5}\frac{\delta z_5}{\delta w_{53}}=(y_5-y_a)(f(z_5)(1-f(z_5)))y_3=(0.69-0.5)(0.69*(1-0.69))*0.663=0.2711
$$
在后面计算例如$w_{31}$得到权值修正时,会遇到$w_{53}$参与计算,这时需要一次性更新,即使用旧的$w_{53}$值,因为$W_{31}$计算过程中的其他参数是基于更新前的数值进行的。
Chapter 5 Convolutional Neural Network
ConvNet Topology卷积网络拓扑
多层感知器的改进
CNN是一个前馈神经网络,可以从一个图像中提取拓扑属性,采用反向传播算法训练减少误差
卷积神经网络旨在通过最少的预处理直接从像素图像中识别视觉模式,可以识别多变性图像
由卷积层、下采样层(池化层)和全连接层组成
C卷积层,局部感知,提取局部特征。权重共享。
P池化层,S下采样
F全连接层
局部连接
每个神经元仅与输入神经元的一块区域连接,称为感受野。在图像卷积操作中,神经元在空间维度是局部连接,但在深度上是全部连接。这种局部连接保证了学习后的过滤器能够对于局部的输入特征有较强的响应。
下图为filters卷积核可视化图像

卷积核与图像某一与卷积核相同大小的区域内各个像素点依次相乘后相加求和
stride步长:卷积核每次平移的距离
$$
featuremap_size=\lfloor\frac{image_size-kernel_size+2*padsize}{stride}\rfloor+1
$$
权重共享
权重对于同一深度切片的神经元是共享的,在很大程度上减少参数。共享权重使得图片的底层边缘特征与特征在图中的具体位置无关。在卷积层,通常采用多组卷积核提取不同特征,即对应不同深度切片的特征。
不同于全连接,卷积核只与部分像素点进行权重计算,并且同一卷积核采用相同权重。
池化Pooling
减少原有图像对应像素点的值,保留图像的相对空间位置,减少计算量。
- Max pooling最大池化
- Average pooling平均池化
- Norm pooling范数池化
- 一范数:绝对值之和
- 二范数:平方和开根号
- p-范数:向量元素绝对值的p次方和的1/p次幂
- 无穷范数:所有向量元素绝对值中的最大值
- Log probability pooling对数概率池化
多层卷积的意义:将不同方向上的特征高阶融合
平整化Flattening
将矩阵拉成一个列向量,后放入全连接层。
CNN计算方面
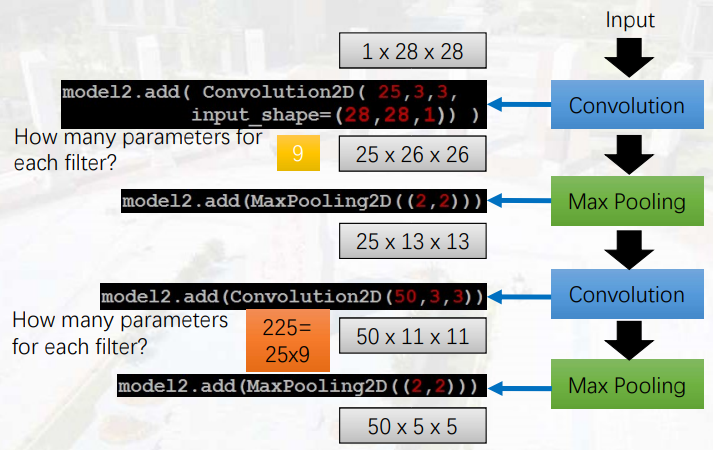
Convolution2D(25, 3, 3)表示有25个大小为3*3的过滤
input_shape(28, 28, 1)表示输入为28*28大小,1为黑白,3为RGB
MaxPooling2D(2,2)表示最大池化层为2*2大小
卷积核的个数决定通道数
Pooling向下取整
25*13*13进行convolution操作,卷积核为50*3*3,首先对于50个卷积核,每个卷积核与25层的13*13大小的像素卷积,后将25层信息叠加为一层,以此得到50*11*11的卷积结果
LeNet网络
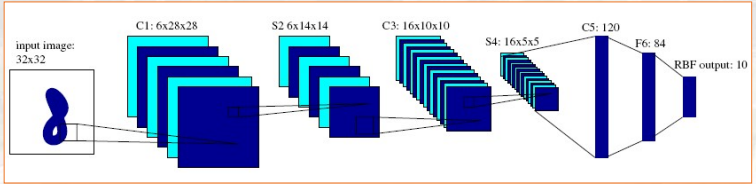

最后RBF输出为10,是因为该问题为数字识别,仅有0~9共10个数字,即为分类问题,输出概率最高数字。
AlexNet网络
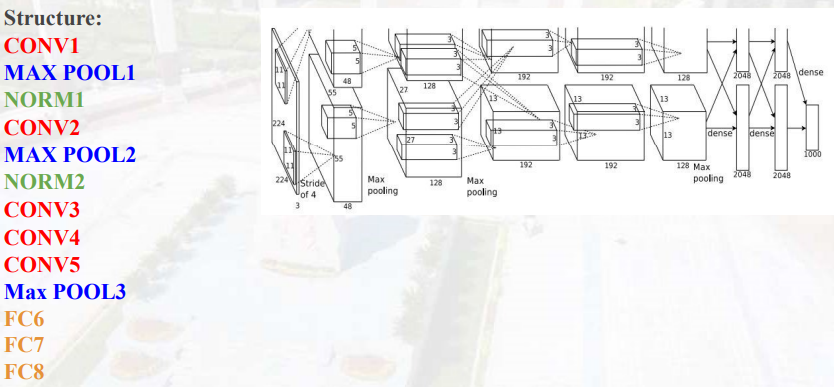
NORM层:归一化、正则化层
创新点

- 使用relu非线性激活函数代替sigmoid激活函数
- 使用dropout操作
- 每一次迭代训练中随机让一些神经元处于不激活状态,避免神经网络过拟合情况
- 使用最大池化而不是平均池化
- 采用LRN
- local response normalization局部响应归一化
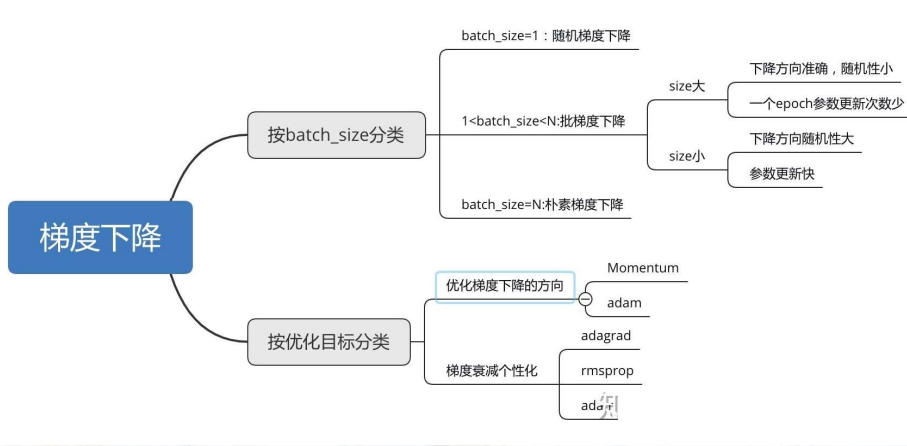
- 采用梯度下降动量法
相关参数计算

第一层输出大小为(227-11)/4+1=55

96 * (3 * 11 * 11) = 34848个权重


池化层没有使用权重,为0!

VGGNet网络
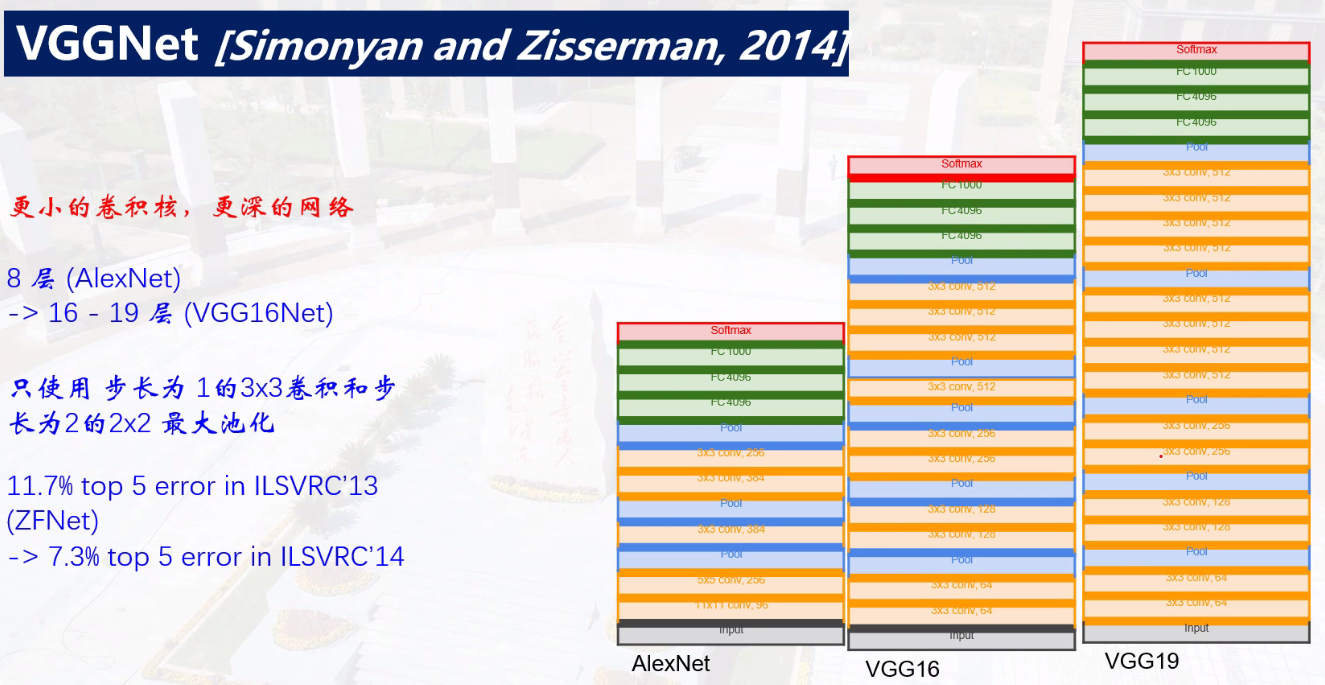
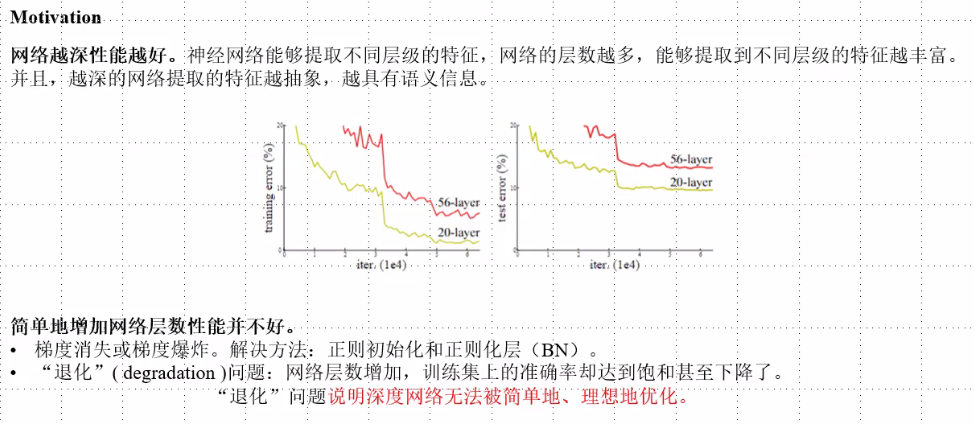
卷积核越来越小,深度越来越深
层过多时:过拟合梯度消失、退化问题严重
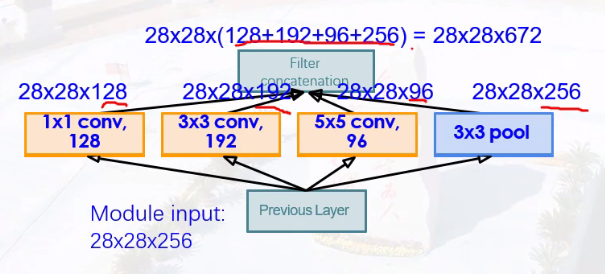
GoogLeNet网络
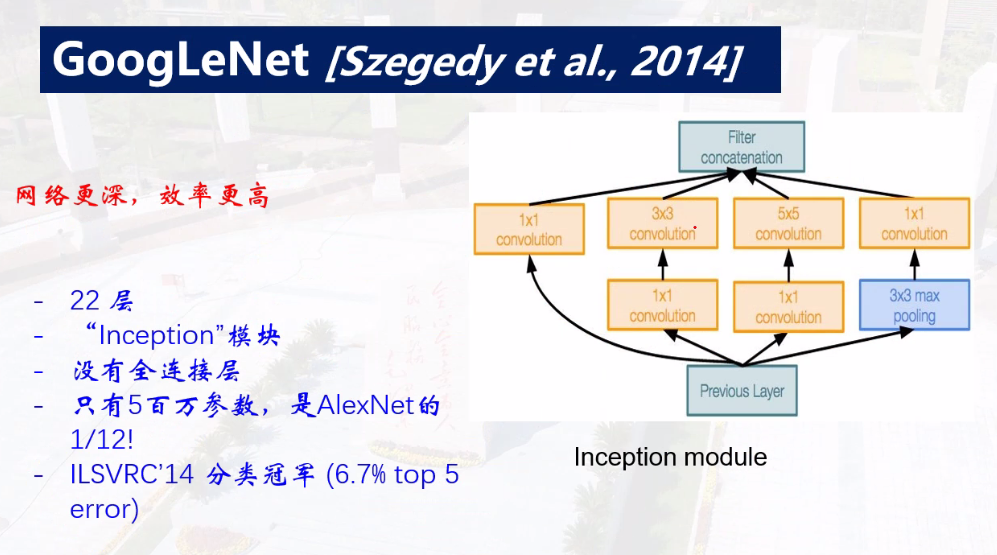
使用不同大小的卷积核(1 * 1,3 * 3,5 * 5)进行级联,提取不同大小细节特征
之后进行Pooling(3 * 3)
concatenation实现通道拼接,将输入填充成相同大小图像,通道数叠加。
但计算量大幅度提高
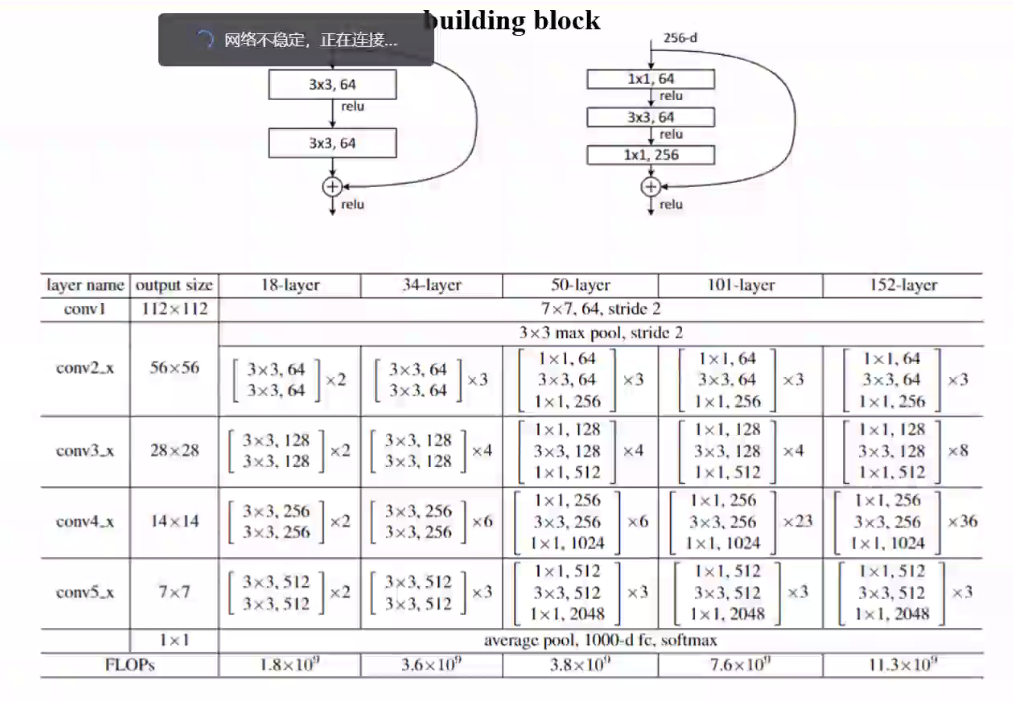
ResNet网络
残差连接
输入和输入的非线性变化的叠加
$$
x_{l+1}=x_l+F(x_l,W_l)
$$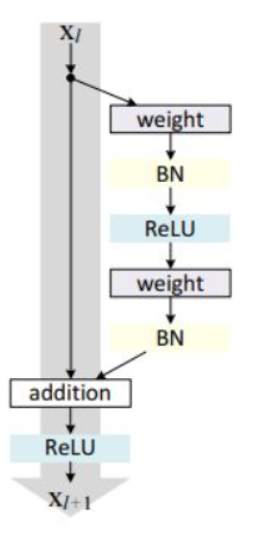
残差块分为两部分,直接映射部分和残差部分。weight代表卷积,addition代表单位加操作。
如果对函数求导,可以看出x的导数为1,另外的F(x,w)导数不可能一直为-1,所以不会出现梯度消失问题。
在卷积网络中$x_l$和$x_{l+1}$可能存在维度不一样的问题,对x进行1*1卷积便于运算,即$x_{l+1}=h(x_l)+F(x_l,W_l)$,其中h为1*1卷积运算。
优化器选择是否进行残差连接操作
DenseNet网络
与ResNet前一层与后一层的短路连接不同,DenseNet建立密集连接,每个层都会与前面所有层在channel维度上连接在一起。
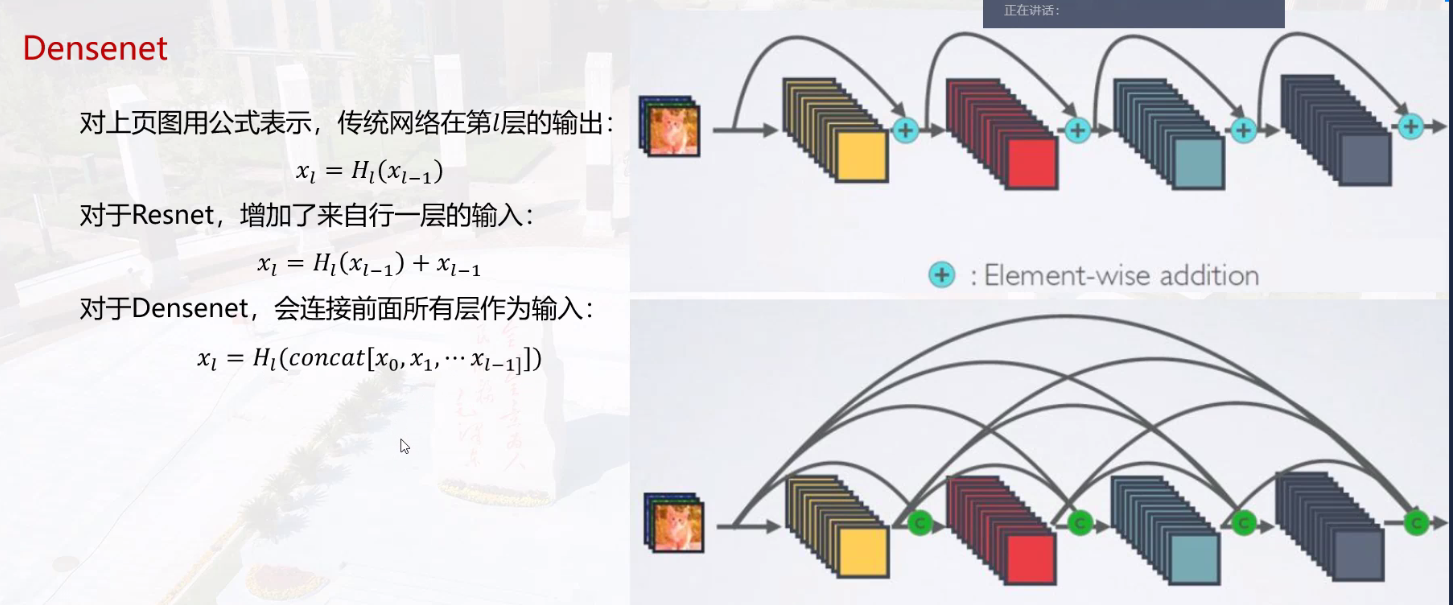
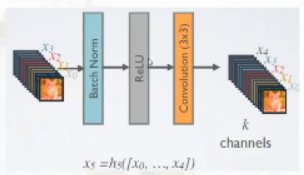
CNN网络一般采用Pooling或者Conv层来降低特征图的大小,而DenseNet采用DenseBlock+Transition的结构。每个层的特征图大小相同,层与层之间采用密集连接方式。
DenseBlock内部结构
Chapter 6 Recurrent Neural Network
序列数据
时间序列数据是指在不同时间点采集到的数据,它反映了某一事物或现象随时间变化的状态或程度。
顺序数据可能不会随时间变化(例如文本序列),但顺序数据总是有一个特征:后一个数据与前一个数据相关。
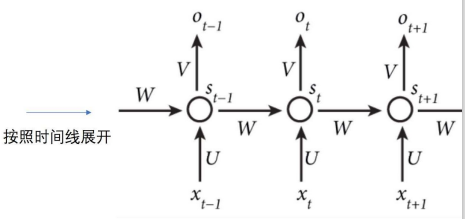
循环神经网络
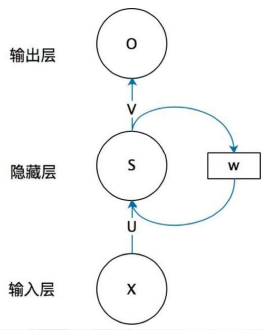
- X:input layer neuron value (它表示输入层的值)
- U:the weight between input layer to hidden layer(输入层到隐藏层的权重)
- S:the hidden layer neuron value(它表示隐藏层)
- O:the output layer neuron value(它表示输出层)
- V:the weight between hidden layer to input layer(隐藏层到输出层的权重)
 $$
O_t=g(V*S_t)
$$
$$
O_t=g(V*S_t)
$$
$$
S_t=f(UX_i+WS_{t-1})
$$
$S_t$的值不仅仅取决于$X_t$,还取决于$S_{t-1}$
序列过程
小练习
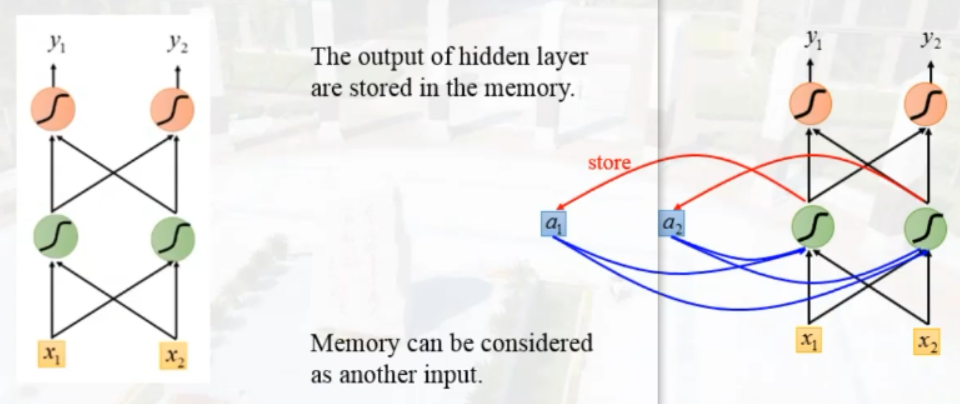

经过三个时刻的变化,求出第一时刻、第二时刻、第三时刻的y1、y2的输出
答案为:[4,4]->[12,12]->[32,32]
Long Short Term Memory(LSTM)
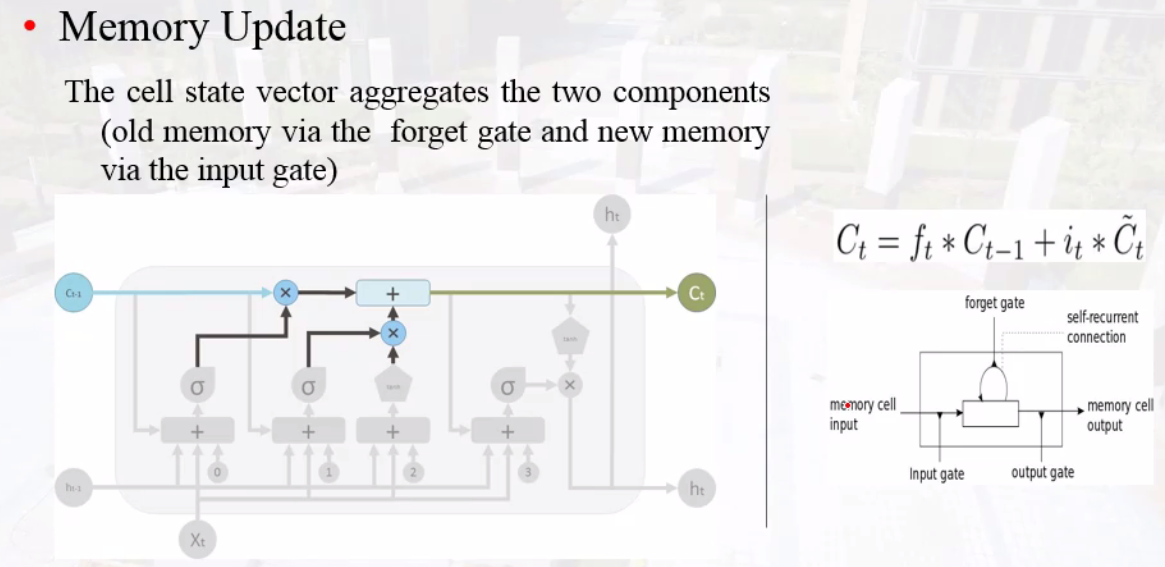
记忆单元memory cell
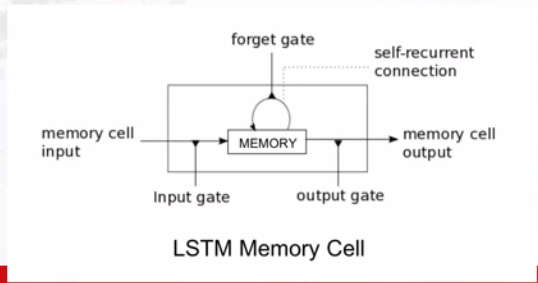
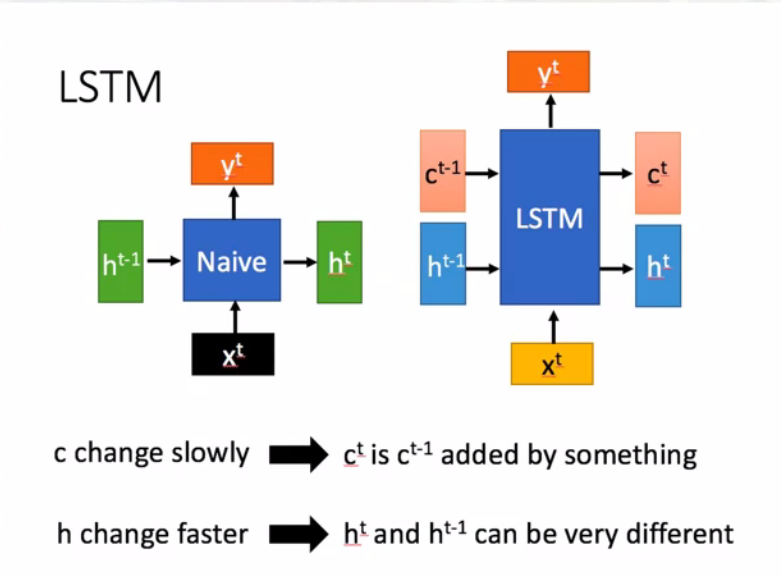
网络结构
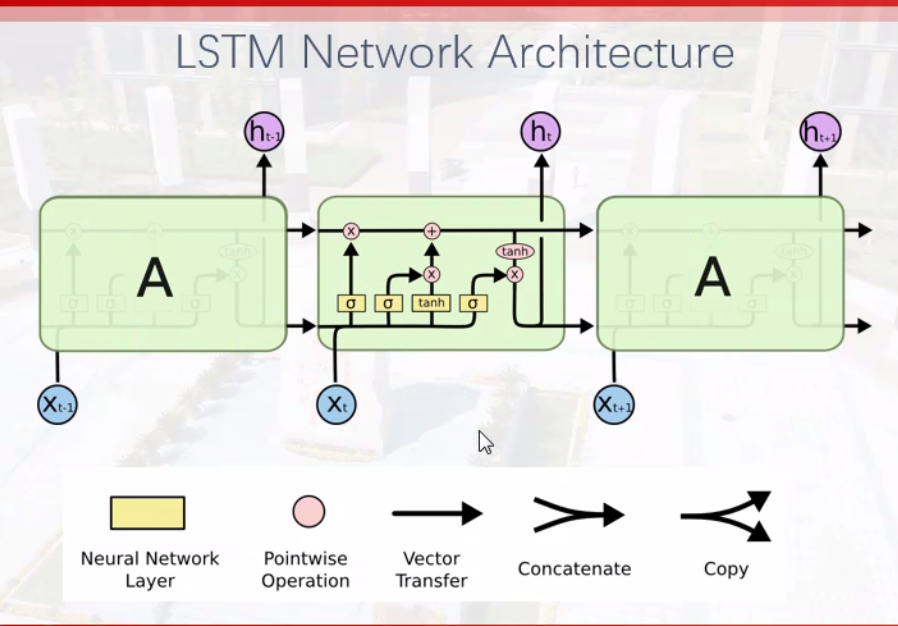
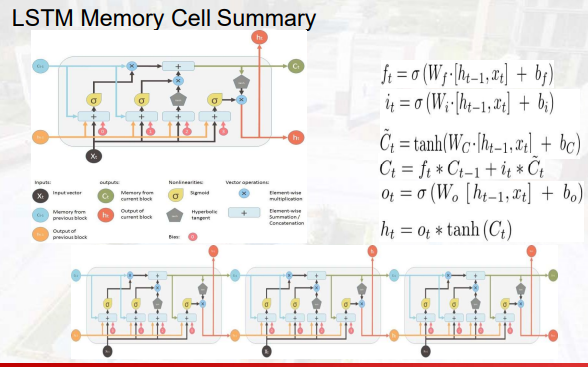
gate门单元

forget gate
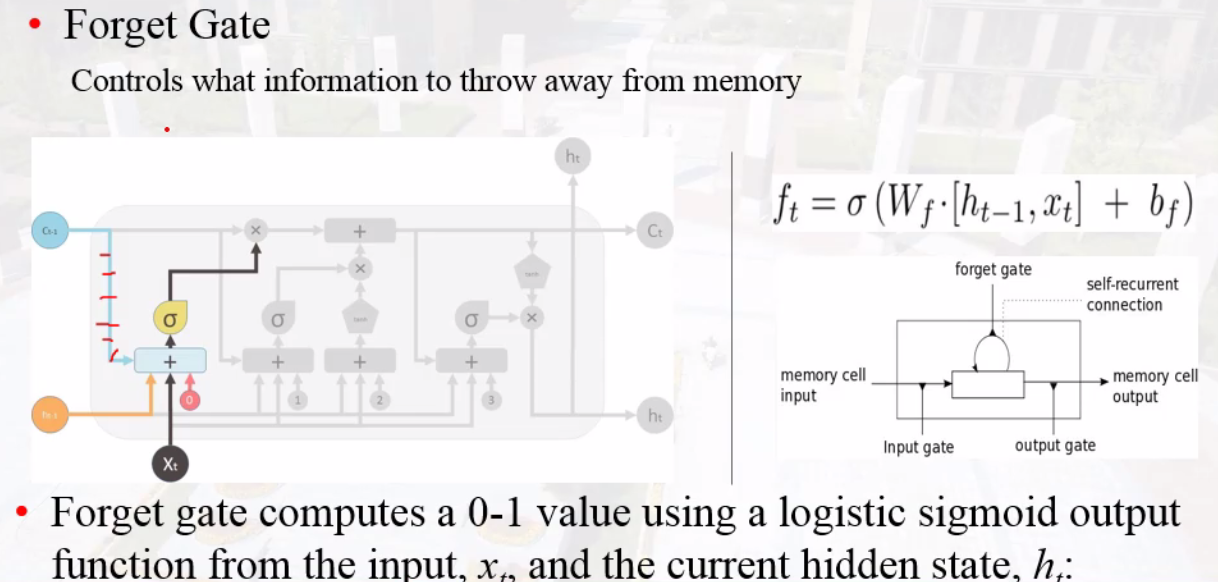

历史信息与当下信息的相关性
input gate
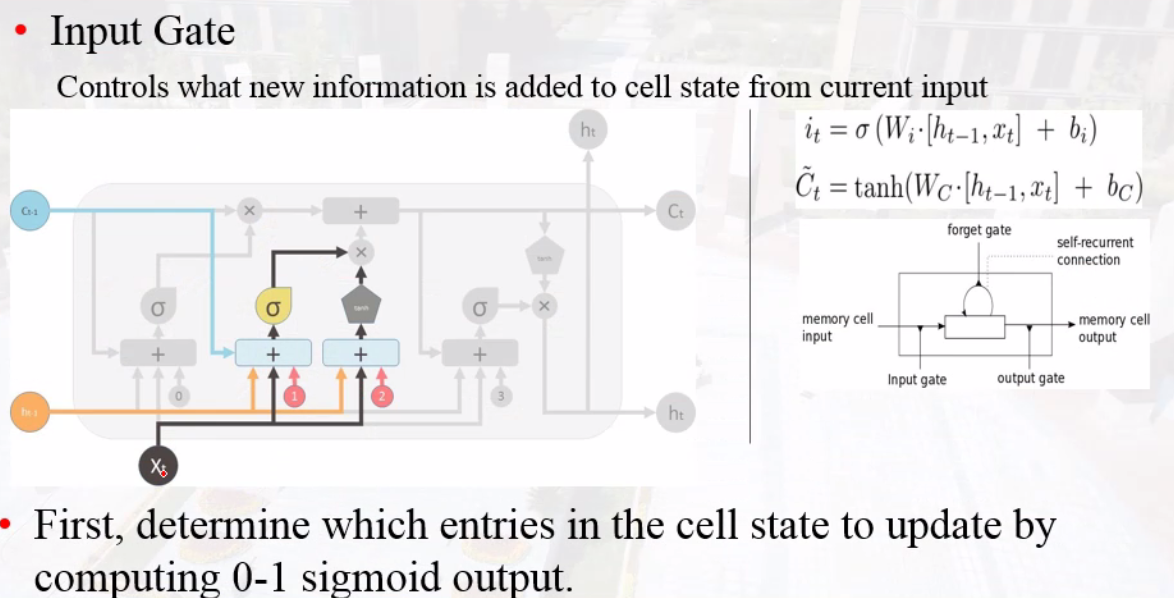
输入信息与历史信息的相关性

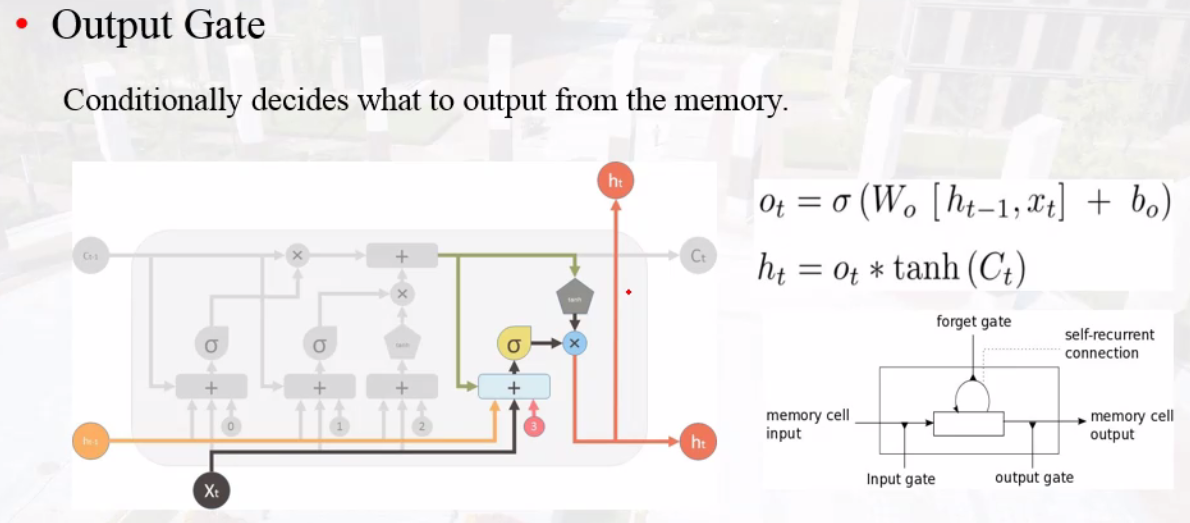
output gate
bos begin of sentense
ens end of sentense
再回顾
上面的内容因为是课堂随笔记的,显得有些乱,不如直接看课件。下面的内容为复习时的所思所想
激活函数优缺点
优点:可以将连续值映射到0到1之间,将问题转化为概率问题,值大于0.5时是正例。
缺点:可能导致梯度消失和梯度爆炸问题;因为其中含有幂运算,所以计算机处理时会很耗时。
什么是线性可分离和不可分离
假设现在有一堆训练数据,它们是由两类点组成的,其中一类点用三角符号画在坐标系中,另一类点用圆圈画在坐标系中。现在拿出直尺和笔在坐标系中画一条直线,如果可以把三角点分到直线的一边,圆圈点分到直线的另一边的话,就说这个训练数据是线性可分的;否则,数据就是线性不可分的。
深度学习中epoch、iteration和batchsize的含义
batchsize批大小
batch_size将影响到模型的优化程度和速度,为了在内存效率和内存容量之间寻找最佳平衡。
适当的增加Batch_Size的优点:
- 通过并行化提高内存利用率。
- 单次epoch的迭代次数减少,提高运行速度。(单次epoch=(全部训练样本/batchsize)/iteration=1)
- 适当的增加Batch_Size,梯度下降方向准确度增加,训练震动的幅度减小。
iteration迭代
1个iteration等于使用batchsize个样本训练一次,训练过程为一个正向传递和一个反向传递。
epoch时期
1个epoch等于使用训练集中的全部样本训练一次,即所有训练样本的一个正向传递和一个反向传递






