线性时不变系统的描述方法关系研究
连续线性时不变系统的描述方法关系研究（有错误！！）
一般认为，系统是指若干相互关联、相互作用的事物按一定规律组合而成的具有特定功能的整体。线性时不变系统由离散和连续时间组成。在连续系统中，信号多由微分方程表示；在离散系统中，信号多由差分方程表示。其中线性系统包含时间域、频率域、s域模型，离散系统包含时间域、z域模型。并且均可用相对应变换的系统框图、信号流图以及状态方程与输出方程表示。离散系统与线性系统在某种程度上很相似，故本文针对线性系统着重讨论。
信号与系统在对电路的分析中应用较广，故以下讨论围绕连续线性时不变系统的电路展开。在电子系统中，系统通常是电子线路，信号通常是随时间变化的电压或电流。从数学观点考虑，这类信号是独立变量t的函数f(t)。
一、连续系统描述方法讨论
(1)数学方程表示
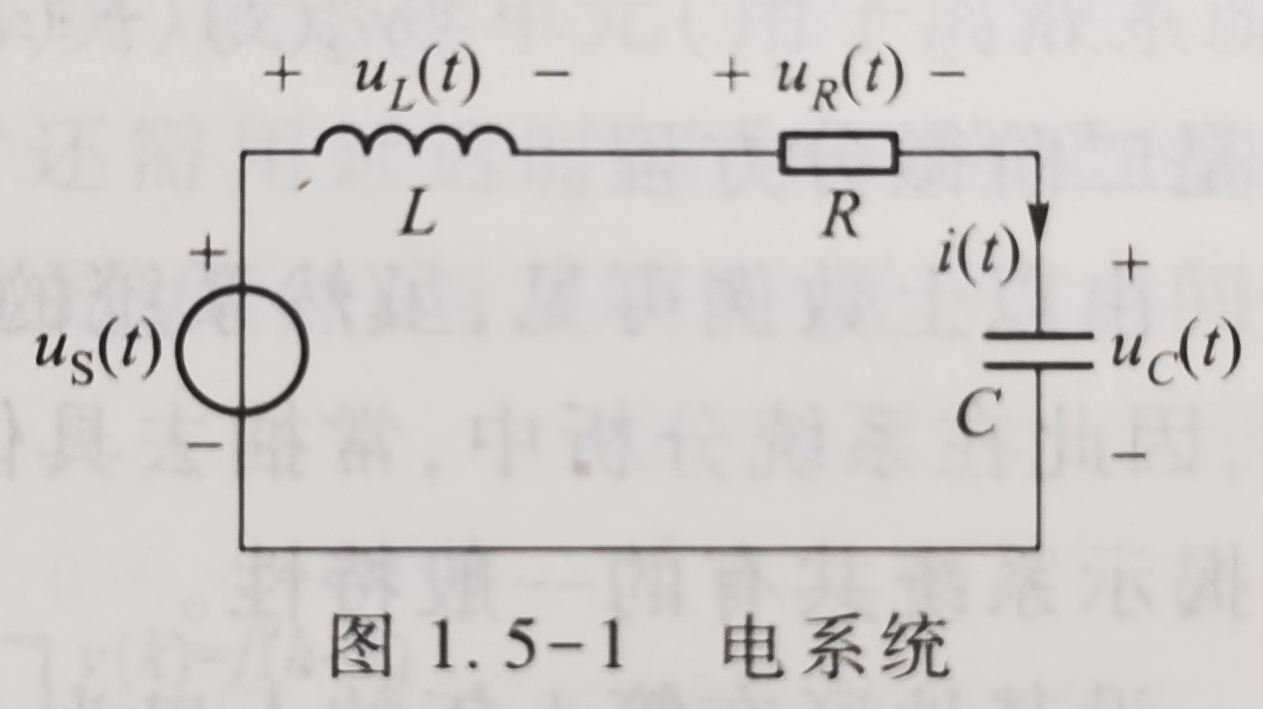
取自课本23页，图1.5-1所示为RLC串联电路。将电压源Us(t)看作是激励，选电容两端电压Uc(t)为响应。
1.时域方程
由基尔霍夫电压定律（KVL）有：
 |
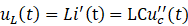（1.1-1） |
|---|
根据各元件电压和电流的关系，得
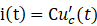
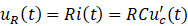
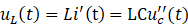
将它们带入式（1.1-1）中并稍加整理，得
 |
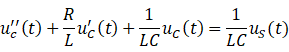（1.1-2） |
|---|
它是二阶线性微分方程，为求得该方程的解，还需已知初始条件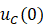
和
。
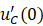2.频域方程
图1.5-1所示得RLC网络得频率响应函数为。其中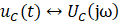
和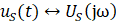
分别为一对傅里叶变换对。
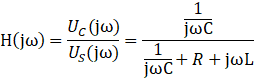
则有
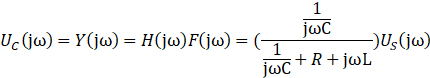
3.s域方程
将式（1.1-2）进行拉普拉斯变换得。其中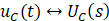
和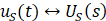
分别为一对拉普拉斯变换对
 |
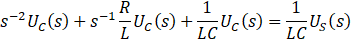（1.3-1） |
|---|
则系统函数可得
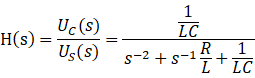
（2）系统框图表示
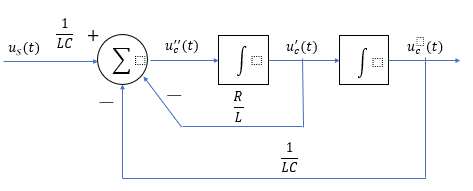
1.时域框图
根据式（1.1-2），可根据时域方程推算出时域框图。
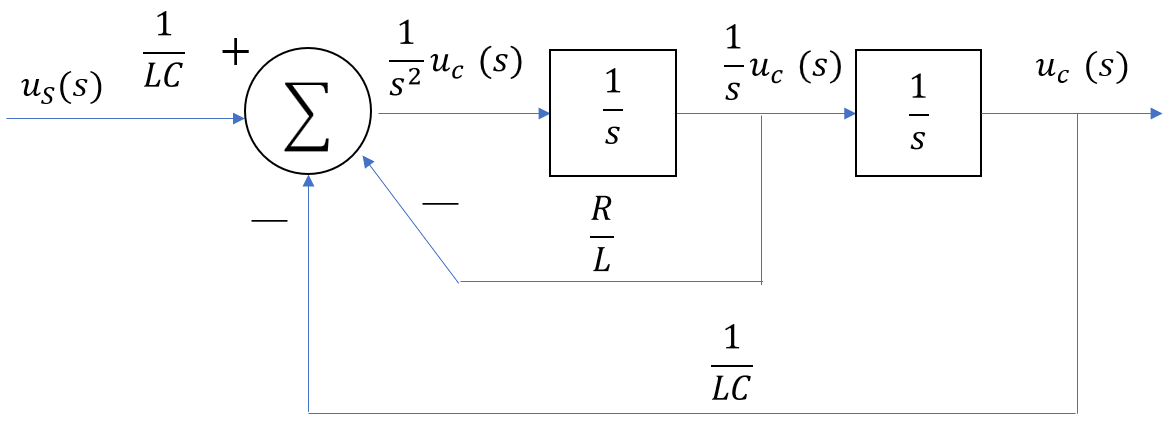
2.s域框图
根据式（1.3-1），可根据s域方程推算出s域框图。
(3)信号流图表示
将系统函数化简为
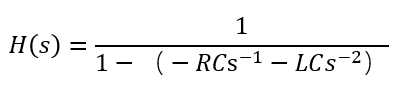
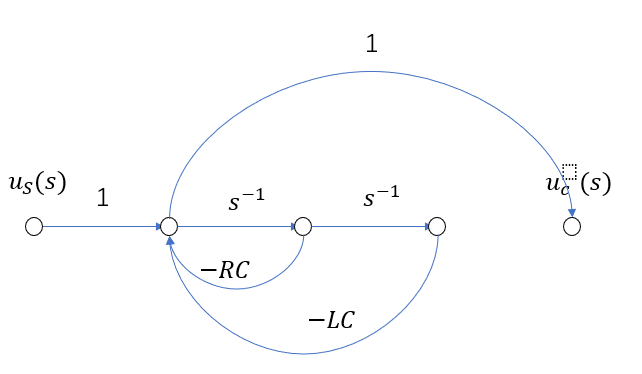
由梅森公式可以很方便的求出信号流图。
（4）状态变量与状态方程表示
电路如图所示，以电阻上的电压$u_R(t)$为输出，列写电路的状态方程和输出方程
根据电路图可知，选取状态变量$x_1 (t)=i_L (t)$和$x_2 (t)=u_C (t)$。
对电路图中的网孔回路列写KVL方程，有$L (di_L (t))/dt)+Ri_L(t)+u_c(t)=u_s(t)$，
得到$x_1^{‘}(t)=-(R/L)x_1(t)+(1/L)x_2(t)+(1/L)u_s(t)$。
对于$u_c(t)$，有$C (du_C (t))/dt)=i_L (t)$,即$x_2^{‘}(t)=(1/C)x_1(t)$。
整理成矩阵形式得
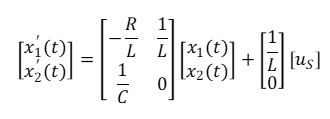
由于流过R上得电流为$x_1(t)$，故其上电压为
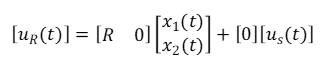
二、连续系统分析方法讨论
（1）LTI系统的时域分析
优点：物理概念清晰，比较直观的得出系统的波形，而且便于数值计算。易于判断系统的因果性。利用卷积易于求得响应，描述系统简单，方便，直观。
缺点：对于大规模电路列写微分方程麻烦,解微分方程更不容易;需要求解初始值。不易计算卷积，尤其是一些复杂函数的卷积
（2）LTI系统的变换域分析
1、频域分析
优点：把信号转换成频率后，可以对LTI系统的频率进行分析。频域分析是信号分析和处理的有效工具。通过傅里叶分析可以判断系统为何种滤波网络。
2、连续系统的S域分析
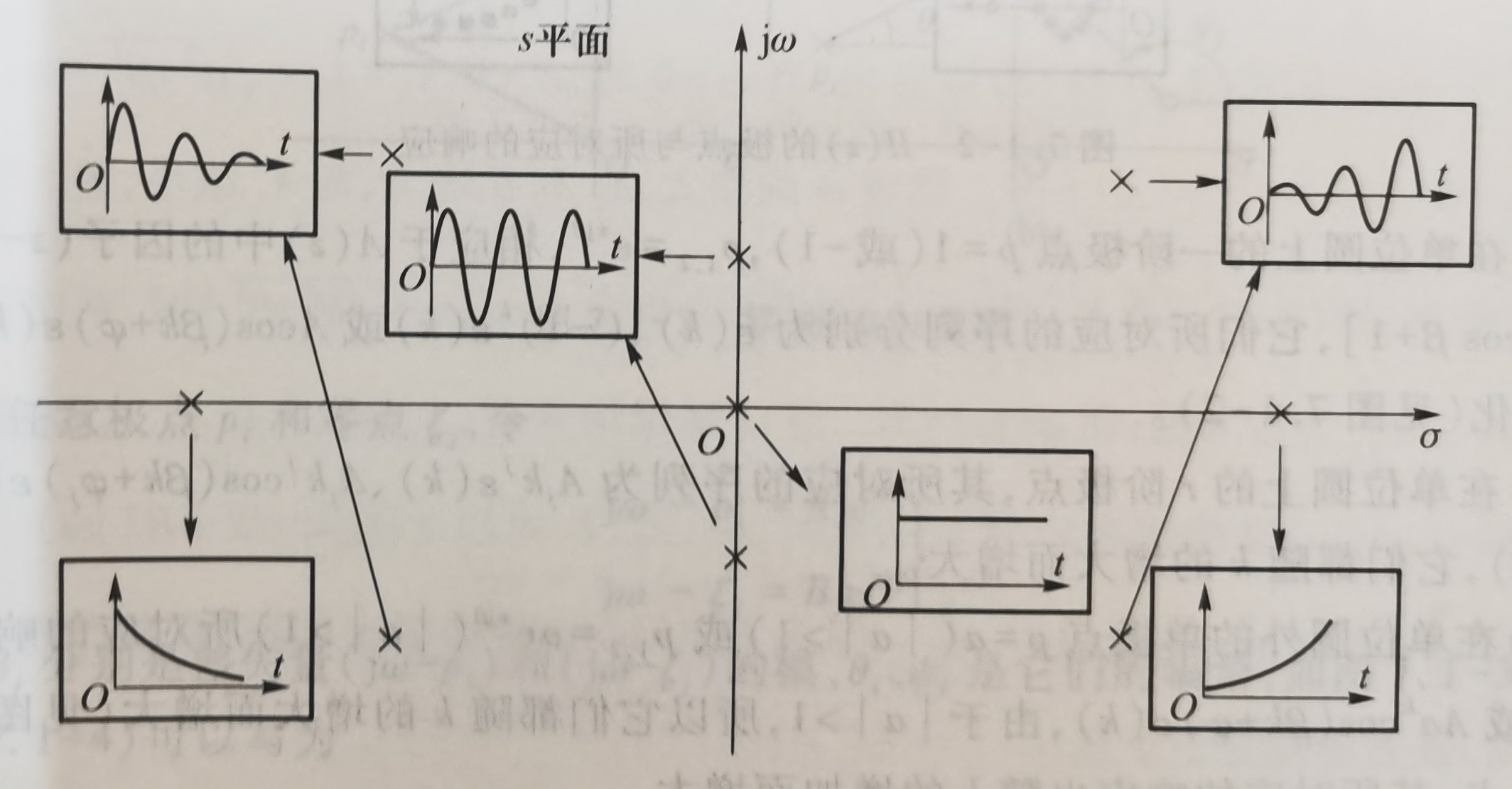
优点：求解的步骤得到简化；拉氏变换把微分或积分运算化为乘法或除法运算，即微分方程化为代数方程；可以很好地分析系统的稳定性，零极点。
