全错位排列模型
错位全排列的概率
摘要:
本文针对错位全排列的概率进行探究,先从基本的问题进行考虑,并拓展到N=n的情况,应用所学的容斥原理对其公式进行推导及证明,并对公式进行近似处理,得到估计公式。
关键词:
错位全排列,概率,容斥原理,一般计算公式,估计公式
引言:
“装错信封问题”是由当时最有名的数学家约翰·伯努利(Johann Bernoulli,1667-1748)的儿子丹尼尔·伯努利(Danid Bernoulli,1700-1782)提出来的,大意如下:一个人写了n封不同的信及相应的n个不同的信封,他把这n封信都装错了信封,问都装错信封的装法有多少种?
全错位排列被著名数学家欧拉(Leonhard Euler,1707-1783)称为“组合数论的一个妙题”的“装错信封问题”的两个特例。
正文:
我们将这个问题与所学概率论与数理统计的相关知识相结合,探究其出现错位全排列的概率。
证明方法
1****、枚举法
对于情况较少的排列,我们可以使用枚举法。
当n=1时,全排列只有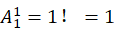 种,不会出现错排情况,D1=0,
种,不会出现错排情况,D1=0,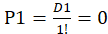 。
。
当n=2时,全排列有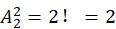 种,即(1、2)和(2、1),其中(2,1)是错排的情况,D2=1,
种,即(1、2)和(2、1),其中(2,1)是错排的情况,D2=1,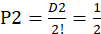 。
。
当n=3时,全排列有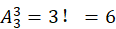 种,即(1、2、3);(1、3、2);(2、1、3);(2、3、1);(3、1、2);(3、2、1),其中只有有(3、1、2)和(2、3、1)是错排,D3=2,
种,即(1、2、3);(1、3、2);(2、1、3);(2、3、1);(3、1、2);(3、2、1),其中只有有(3、1、2)和(2、3、1)是错排,D3=2,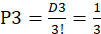 。
。
当n=4时,全排列有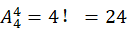 种,即(1、2、3、4);(1、2、4、3);(1、3、2、4);(1、3、4、2);(1、4、2、3);(1、4、3、2);(2、1、3、4);(2、1、4、3);(2、3、1、4);(2、3、4、1);(2、4、1、3);(2、4、3、1);(3、1、2、4);(3、1、4、2);(3、2、1、4);(3、2、4、1);(3、4、1、2);(3、4、2、1);(4、1、2、3);(4、1、3、2);(4、2、1、3);(4、2、3、1);(4、3、1、2);(4、3、2、1),发现其中(2、1、4、3);(2、3、4、1);(2、4、1、3);(3、1、4、2);(3、4、1、2);(3、4、2、1);(4、1、2、3);(4、3、1、2);(4、3、2、1)是错排的情况,D4=9,
种,即(1、2、3、4);(1、2、4、3);(1、3、2、4);(1、3、4、2);(1、4、2、3);(1、4、3、2);(2、1、3、4);(2、1、4、3);(2、3、1、4);(2、3、4、1);(2、4、1、3);(2、4、3、1);(3、1、2、4);(3、1、4、2);(3、2、1、4);(3、2、4、1);(3、4、1、2);(3、4、2、1);(4、1、2、3);(4、1、3、2);(4、2、1、3);(4、2、3、1);(4、3、1、2);(4、3、2、1),发现其中(2、1、4、3);(2、3、4、1);(2、4、1、3);(3、1、4、2);(3、4、1、2);(3、4、2、1);(4、1、2、3);(4、3、1、2);(4、3、2、1)是错排的情况,D4=9,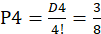 。
。
2****、递推数列法
由于枚举所有情况较为繁琐,且容易遗漏,在N较小的情况下,可以用以下的想法考虑。并用例题辅助证明。
例题1:
甲、乙、丙、丁各做一张卡片,送给其他人,求送的卡片全部错开的概率?
解题思路:
第一步:从甲开始送卡片,可以送给乙、丙、丁三个人,故有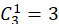 种送法。由于乙、丙、丁三个人满足轮换情况,故可假定送给丁,送给乙、丙的情况同理。
种送法。由于乙、丙、丁三个人满足轮换情况,故可假定送给丁,送给乙、丙的情况同理。
第二步:
第一类:丁送给甲卡片,剩下两个人互送,即有D2=1种送法。
第二类:丁可送给乙、丙二人,有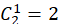 种送法。由于乙、丙两个人轮换,故可假定送给丙,送给乙的情况同理。
种送法。由于乙、丙两个人轮换,故可假定送给丙,送给乙的情况同理。
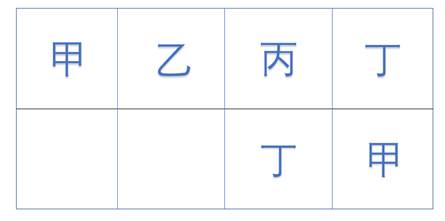
如图,由于乙不能送给自己,故只能选择送给甲,丙的卡片送给乙,满足题意。
综上所述,由于全排列有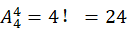 种,全错位排列共有
种,全错位排列共有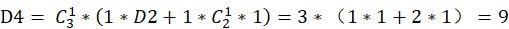 种情况,则所求送的卡片全部错开的概率为
种情况,则所求送的卡片全部错开的概率为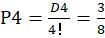 。
。
例题2:
有编号1,2,3,4,5的五个球和编号为1,2,3,4、5的五个盒子,每个盒子内投放一球,且且与盒子的编号不相同,有多少种投放办法?
解题思路:
第一步:编号为1的球共有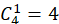 种盒子选择,由于剩下的2、3、4、5号盒子具有轮换性,可假定编号为一的球放在了5号盒子内,选择其他盒子的情况同理。
种盒子选择,由于剩下的2、3、4、5号盒子具有轮换性,可假定编号为一的球放在了5号盒子内,选择其他盒子的情况同理。
第二步:
第一类:5号盒子内装了1号的球,剩下三个盒子2,3,4共有球的编号为(3,4,2)和(4,2,3)即D3=2种装法。
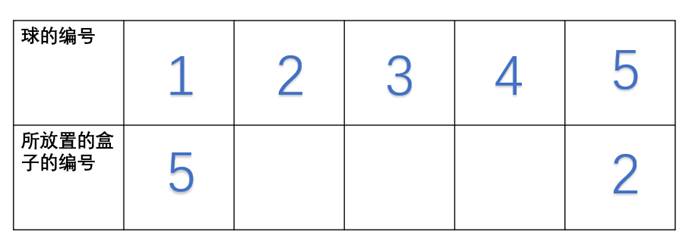 第二类:5号盒子内装了2,3,4的球,共有
第二类:5号盒子内装了2,3,4的球,共有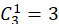 种选择,由轮换性可知,可假定编号为5的球放进了2号盒子内,选择其他盒子的情况同理。
种选择,由轮换性可知,可假定编号为5的球放进了2号盒子内,选择其他盒子的情况同理。
如图所示,此时剩余的三个空格有(1,4,3)和(4,1,3)和(3,4,1)三种填法满足题意
综上所述,由于全排列有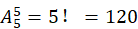 种,全错位排列共有
种,全错位排列共有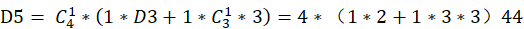 种情况,则所求送的卡片全部错开的概率为
种情况,则所求送的卡片全部错开的概率为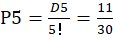 。
。
归纳总结:
显然D1=0,D2=1。当n>=3时,不妨设n排在了第k位,其中k≠n,也就是1<=k<=n-1。那么考虑第n位的情况。
1、当k排在第n位时,除了n和k以外还有n-2个数,其错排数为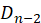 。
。
2、当k不排在第n位时,那么将第n位重新考虑成一个新的“第k位”,这时的包括k在内的剩下n-1个数的每一种错排,都等价于只有n-1个数时的错排(只是其中的第k位会换成第n位)。其错排数为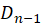 。
。
所以当n排在第k位时共有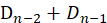 种错排方法,又k有从1到n-1共n-1种取法,我们可以得到:
种错排方法,又k有从1到n-1共n-1种取法,我们可以得到:
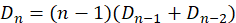
在上面我们得到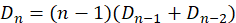 ,从这个公式中我们可以推出
,从这个公式中我们可以推出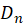 的通项公式,方法如下:
的通项公式,方法如下:
为书写方便,记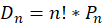 ,则
,则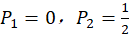 。
。
当n>=3时,由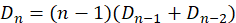 ,
,
即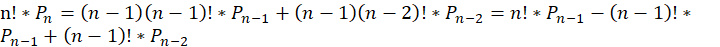 ,
,
所以有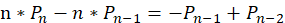 。
。
于是有
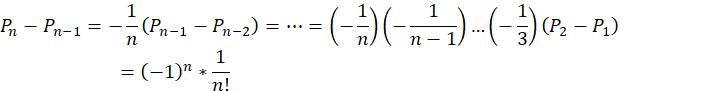
将上面式子分边累加,得
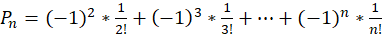 ,
,
即为我们所求的错位全排列出现的概率。
容斥原理证明法
首先我们总结归纳出容斥原理:
根据概率论与数理统计课本上的加法公式:设A、B是事件,则有
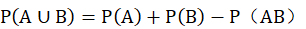
对加法公式进行证明:由于
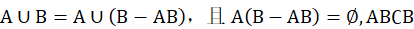
由有限可加性公式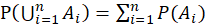 及减法公式
及减法公式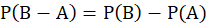 得
得
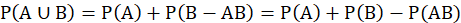
当有A、B、C三个事件时,则有
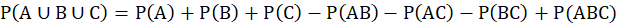
故可归纳总结出一般性的容斥原理
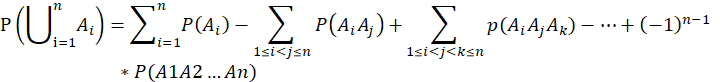
使用数学归纳法进行证明:
当n=2时,等式成立(加法公式)
假设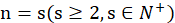 时结论成立,则当n=s+1时
时结论成立,则当n=s+1时
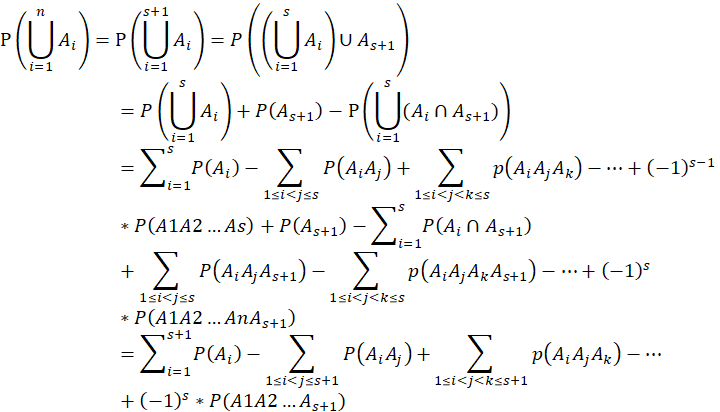
所以当n=s+1时,结论仍成立。因此对任意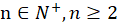 ,均可使所证等式成立。
,均可使所证等式成立。
现使用所证得的容斥原理对公式证明
设1,2,…,n的全排列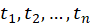 的集合为I,而使
的集合为I,而使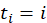 的全排列的集合记为
的全排列的集合记为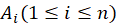 ,则
,则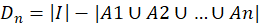 ,所以
,所以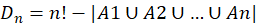 ,则
,则
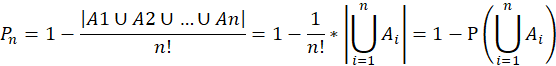
注意到当有1个元素排对时,剩下的n-1个元素进行全排列得到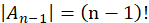 ,并且满足这样要求的集合组共有
,并且满足这样要求的集合组共有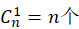 。则
。则
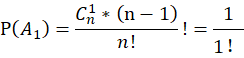
当有2个元素排对时,剩下的n-2个元素进行全排列得到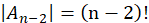 ,并且满足这样要求的集合组共有
,并且满足这样要求的集合组共有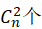 。则
。则
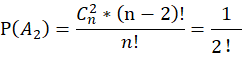
以此类推,当有i个元素排对时(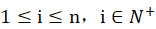 ),剩下的n-i个元素进行全排列得到
),剩下的n-i个元素进行全排列得到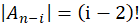 ,并且满足这样要求的集合组共有
,并且满足这样要求的集合组共有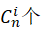 。则
。则
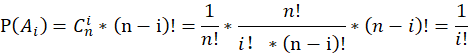
因此由容斥原理有
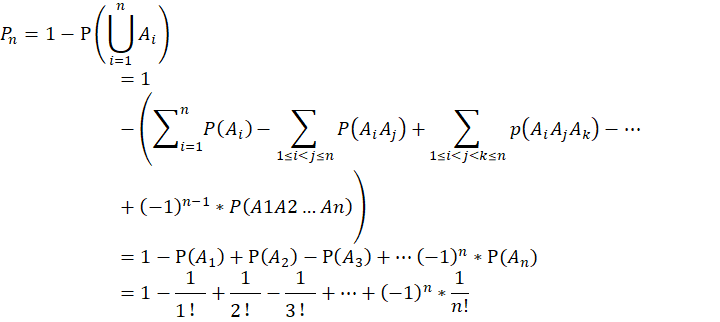
得证
错位全排列概率的估计
概率的近似值
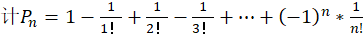
我们可以使用python编程计算当n近似无穷大时所求的概率
当n=3时,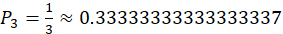 ,
,
当n=10时,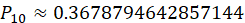 ,
,
当n=30时,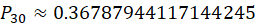 ,
,
当n=100时,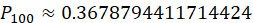 ,
,
当n=1000时,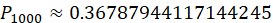 ,
,
会发现概率会无限趋近于0.36787944117144233,这恰恰是 的值。
的值。
在高等数学当中,函数 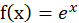 的麦克劳林公式(Maclaurin’s series)如下:
的麦克劳林公式(Maclaurin’s series)如下:
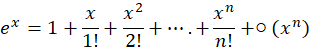
代入x=-1得:
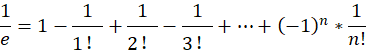
所以我们可以得出
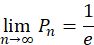
估计公式
由以上的级数,可以得到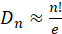 ,但是由于麦克劳伦公式是有一个“余项”存在的,总会有一定的误差。那么误差有多大呢?
,但是由于麦克劳伦公式是有一个“余项”存在的,总会有一定的误差。那么误差有多大呢?
记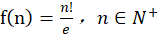 ,接下来同样借助python编程来估计误差。
,接下来同样借助python编程来估计误差。
当n=1时,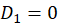 ,而
,而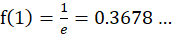
当n=2时,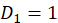 ,而
,而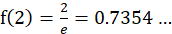
当n=3时,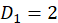 ,而
,而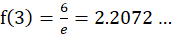
当n=4时,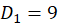 ,而
,而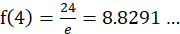
当n=5时,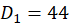 ,而
,而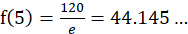
当n=6时,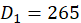 ,而
,而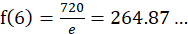
当n=7时,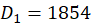 ,而
,而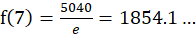
从上面的数据可以看出,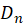 的值实际上是
的值实际上是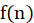 四舍五入的结果。因此可以将
四舍五入的结果。因此可以将 改写成:
改写成: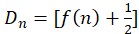 ,其中
,其中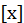 表示不超过x的最大整数。
表示不超过x的最大整数。
所以得到估计公式: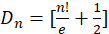 。
。
在平常计算当中,使用此公式可以大大缩短计算时间,非常便利。





